| Issue |
ESAIM: M2AN
Volume 53, Number 1, January–February 2019
|
|
|---|---|---|
| Page(s) | 105 - 144 | |
| DOI | https://doi.org/10.1051/m2an/2018069 | |
| Published online | 02 April 2019 | |
Research Article
Stability analysis and error estimates of arbitrary Lagrangian–Eulerian discontinuous Galerkin method coupled with Runge–Kutta time-marching for linear conservation laws
1
School of Mathematics and Information Science, Henan Polytechnic University, 454003 Jiaozuo, Henan, PR China
2
School of Mathematical Sciences, University of Science and Technology of China, 230026 Hefei, Anhui, PR China
3
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
* Corresponding author: yhxia@ustc.edu.cn
Received:
8
March
2018
Accepted:
2
November
2018
In this paper, we discuss the stability and error estimates of the fully discrete schemes for linear conservation laws, which consists of an arbitrary Lagrangian–Eulerian discontinuous Galerkin method in space and explicit total variation diminishing Runge–Kutta (TVD-RK) methods up to third order accuracy in time. The scaling arguments and the standard energy analysis are the key techniques used in our work. We present a rigorous proof to obtain stability for the three fully discrete schemes under suitable CFL conditions. With the help of the reference cell, the error equations are easy to establish and we derive the quasi-optimal error estimates in space and optimal convergence rates in time. For the Euler-forward scheme with piecewise constant elements, the second order TVD-RK method with piecewise linear elements and the third order TVD-RK scheme with polynomials of any order, the usual CFL condition is required, while for other cases, stronger time step restrictions are needed for the results to hold true. More precisely, the Euler-forward scheme needs τ ≤ ρh2 and the second order TVD-RK scheme needs 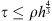 for higher order polynomials in space, where τ and h are the time and maximum space step, respectively, and ρ is a positive constant independent of τ and h.
for higher order polynomials in space, where τ and h are the time and maximum space step, respectively, and ρ is a positive constant independent of τ and h.
Mathematics Subject Classification: 65M60 / 35L65 / 65M12
Key words: Arbitrary Lagrangian–Eulerian discontinuous Galerkin method / Runge–Kutta methods / stability / error estimates / conservation laws
© The authors. Published by EDP Sciences, SMAI 2019
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


