| Issue |
ESAIM: M2AN
Volume 39, Number 6, November-December 2005
|
|
|---|---|---|
| Page(s) | 1203 - 1249 | |
| DOI | https://doi.org/10.1051/m2an:2005047 | |
| Published online | 15 November 2005 | |
A finite volume method for the Laplace equation on almost arbitrary two-dimensional grids
1
Mathématiques pour l'Industrie et la
Physique, Université Paul Sabatier, 118 route de Narbonne,
31062 Toulouse Cedex 4, France. komla@mip.ups-tlse.fr
2
Commissariat à l'Énergie Atomique,
DEN-DM2S-SFME, 91191 Gif-sur-Yvette Cedex, France. pascal.omnes@cea.fr
Received:
26
April
2004
Revised:
7
July
2005
We present a finite volume method based on the integration of the Laplace
equation on both the cells of a primal almost arbitrary two-dimensional
mesh and those of a
dual mesh obtained by joining the centers of the cells of the primal mesh.
The key ingredient is the definition of discrete gradient and divergence
operators verifying a discrete Green formula.
This method generalizes an existing finite volume method that
requires “Voronoi-type” meshes.
We show the equivalence of this finite volume method with a non-conforming
finite element method with basis functions being P1 on the cells,
generally called “diamond-cells”, of a third mesh.
Under geometrical conditions on these diamond-cells,
we prove a first-order convergence both in the 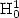 norm
and in the L² norm.
Superconvergence results are obtained on certain types of homothetically refined grids.
Finally, numerical experiments confirm these results and also show second-order convergence
in the L² norm on general grids.
They also indicate that this method performs particularly well for the approximation
of the gradient of the solution, and may be used on degenerating triangular grids.
An example of application on non-conforming locally refined grids is given.
norm
and in the L² norm.
Superconvergence results are obtained on certain types of homothetically refined grids.
Finally, numerical experiments confirm these results and also show second-order convergence
in the L² norm on general grids.
They also indicate that this method performs particularly well for the approximation
of the gradient of the solution, and may be used on degenerating triangular grids.
An example of application on non-conforming locally refined grids is given.
Mathematics Subject Classification: 35J05 / 35J25 / 65N12 / 65N15 / 65N30
Key words: Finite volume method / non-conforming finite element method / Laplace equation / discrete Green formula / diamond-cell / error estimates / convergence / superconvergence / arbitrary meshes / degenerating meshes / non-conforming meshes.
© EDP Sciences, SMAI, 2005
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


