| Issue |
ESAIM: M2AN
Volume 40, Number 3, May-June 2006
|
|
|---|---|---|
| Page(s) | 553 - 595 | |
| DOI | https://doi.org/10.1051/m2an:2006022 | |
| Published online | 22 July 2006 | |
Analysis of crack singularities in an aging elastic material
1
Institut de Recherche
Mathématique de Rennes, Université de Rennes 1,
Campus de Beaulieu,
35042 Rennes Cedex, France.
Martin.Costabel@univ-rennes1.fr; Monique.Dauge@univ-rennes1.fr
2
Institute of Mechanical Engineering Problems,
Laboratory of Mathematical Methods, Russian Academy of Sciences,
V.O. Bol'shoi 61, 199178 St. Petersburg, Russia.
serna@snark.ipme.ru
3
Institut Élie Cartan, Laboratoire de Mathématiques,
Université Henri Poincaré Nancy I,
B.P. 239, 54506 Vandoeuvre-lès-Nancy Cedex, France.
Jan.Sokolowski@iecn.u-nancy.fr
Received:
10
March
2005
We consider a quasistatic system involving a Volterra kernel modelling
an hereditarily-elastic aging body. We are concerned with the behavior of
displacement and stress fields in the neighborhood of cracks. In this paper, we
investigate the case of a straight crack in a two-dimensional domain with a possibly
anisotropic material law.
We study the asymptotics of the time dependent solution near the crack tips.
We prove that, depending on the regularity of the material
law and the Volterra kernel, these asymptotics contain singular functions which
are simple homogeneous
functions of degree 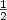 or have a more complicated dependence on
the distance variable r to the crack tips. In the latter situation,
we observe a novel behavior of the singular functions, incompatible with
the usual fracture criteria, involving super polynomial functions
of ln r growing in time.
or have a more complicated dependence on
the distance variable r to the crack tips. In the latter situation,
we observe a novel behavior of the singular functions, incompatible with
the usual fracture criteria, involving super polynomial functions
of ln r growing in time.
Mathematics Subject Classification: 35Q72 / 74D05 / 74G70
Key words: Crack singularities / creep theory / Volterra kernel / hereditarily-elastic.
© EDP Sciences, SMAI, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


