| Issue |
ESAIM: M2AN
Volume 36, Number 1, January/February 2002
|
|
|---|---|---|
| Page(s) | 55 - 68 | |
| DOI | https://doi.org/10.1051/m2an:2002003 | |
| Published online | 15 April 2002 | |
Simultaneous vs. non-simultaneous blow-up in numerical approximations of a parabolic system with non-linear boundary conditions
1
Instituto de Ciencias, Univ. Nac. Gral. Sarmiento, J.M. Gutierrez entre Verdi y J.L. Suarez (1613), Los Polvorines, Buenos Aires, Argentina. gacosta@ungs.edu.ar.
2
Departamento de Matemática, FCEyN, UBA (1428), Buenos Aires, Argentina. jfbonder@dm.uba.ar. andjrossi@dm.uba.ar.
3
Universidad de San Andrés, Vito Dumas 284 (1644), Victoria, Buenos Aires, Argentina. pgroisman@udesa.edu.ar.
Received:
23
April
2001
Revised:
12
October
2001
We study the asymptotic behavior of a semi-discrete numerical
approximation for a pair of heat equations ut = Δu, vt = Δv in Ω x (0,T); fully coupled by the boundary
conditions  ,
, 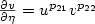 on ∂Ω x (0,T), where
Ω is a bounded smooth domain in
on ∂Ω x (0,T), where
Ω is a bounded smooth domain in  . We focus in the
existence or not of non-simultaneous blow-up for a semi-discrete
approximation (U,V). We prove that if U blows up in finite time
then V can fail to blow up if and only if p11 > 1 and p21 < 2(p11 - 1)
, which is the same condition as the one
for non-simultaneous blow-up in the continuous problem. Moreover,
we find that if the continuous
problem has non-simultaneous blow-up then the same is true for
the discrete one. We also prove some
results about the convergence of the scheme and the convergence
of the blow-up times.
. We focus in the
existence or not of non-simultaneous blow-up for a semi-discrete
approximation (U,V). We prove that if U blows up in finite time
then V can fail to blow up if and only if p11 > 1 and p21 < 2(p11 - 1)
, which is the same condition as the one
for non-simultaneous blow-up in the continuous problem. Moreover,
we find that if the continuous
problem has non-simultaneous blow-up then the same is true for
the discrete one. We also prove some
results about the convergence of the scheme and the convergence
of the blow-up times.
Mathematics Subject Classification: 65M60 / 65M20 / 35K60 / 35B40
Key words: Blow-up / parabolic equations / semi-discretization in space / asymptotic behavior / non-linear boundary conditions.
© EDP Sciences, SMAI, 2002
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


