Free Access
| Issue |
ESAIM: M2AN
Volume 43, Number 1, January-February 2009
|
|
|---|---|---|
| Page(s) | 173 - 208 | |
| DOI | https://doi.org/10.1051/m2an:2008044 | |
| Published online | 05 December 2008 | |
- M. Balabane, J. Dolbeault and H. Ounaies, Nodal solutions for a sublinear elliptic equation. Nonlinear Anal. 52 (2003) 219–237. [CrossRef] [MathSciNet] [Google Scholar]
- A.V. Buryak, V.V. Steblina and Y. Kivshar, Self-trapping of light beams and parametric solitons in diffractive quadratic media. Phys. Rev. A 52 (1995) 1670–1674. [CrossRef] [PubMed] [Google Scholar]
- A.V. Buryak, P. Di Trapani, D.V. Skryabin and S. Trillo, Optical solitons due to quadratic nonlinearities: from basic physics to futuristic applications. Phys. Rep. 370 (2002) 62–235. [Google Scholar]
- L. Di Menza, Transparent and absorbing conditions for the Schrödinger equation in a bounded domain. Numer. Funct. Anal. Optim. 18 (1997) 759–775. [Google Scholar]
- G. Fibich, N. Gavish and X.-P. Wang, Singular ring solutions of critical and supercritical nonlinear Schrödinger equations. Physica D 18 (2007) 55–86. [CrossRef] [Google Scholar]
- W.J. Firth and D.V. Skryabin, Optical solitons carrying orbital angular momentum. Phys. Rev. Lett. 79 (1997) 2450–2453. [CrossRef] [Google Scholar]
- H. He, M.J. Werner and P.D. Drummond, Simultaneous solitary-wave solutions in a nonlinear parametric waveguide. Phys. Rev. E 54 (1996) 896–911. [CrossRef] [Google Scholar]
- J. Iaia and H. Warchall, Nonradial solutions of a semilinear elliptic equation in two dimensions. J. Diff. Equ. 119 (1995) 533–558. [CrossRef] [Google Scholar]
- R. Kajikiya, Norm estimates for radially symmetric solutions of semilinear elliptic equations. Trans. Amer. Math. Soc. 347 (1995) 1163–1199. [CrossRef] [MathSciNet] [Google Scholar]
-
M.K. Kwong, Uniqueness of positive solutions of
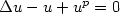in 
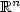. Arch. Rat. Mech. Anal. 105 (1989) 243–266.
[Google Scholar]
- D.J.B. Lloyd and A.R. Champneys, Efficient numerical continuation and stability analysis of spatiotemporal quadratic optical solitons. SIAM J. Sci. Comput. 27 (2005) 759–773. [CrossRef] [MathSciNet] [Google Scholar]
- B. Malomed, P. Drummond, H. He, A. Berntson, D. Anderson and M. Lisak, Spatiotemporal solitons in multidimensional optical media with a quadratic nonlinearity. Phys. Rev. E 56 (1997) 4725–4735. [CrossRef] [Google Scholar]
-
K. McLeod, W.C. Troy and F.B. Weissler, Radial solutions of
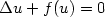with prescribed number of zeros. J. Diff. Equ. 83 (1990) 368–378.
[CrossRef]
[Google Scholar]
- T. Mizumachi, Vortex solitons for 2D focusing nonlinear Schrödinger equation. Diff. Int. Equ. 18 (2005) 431–450. [Google Scholar]
- I.M. Moroz, R. Penrose and P. Tod, Spherically-symmetric solutions of the Schrödinger-Newton equation. Class. Quant. Grav. 15 (1998) 2733–2742. [CrossRef] [Google Scholar]
-
V.V. Steblina, Y. Kivshar, M. Lisak and B.A. Malomed, Self-guided beams in diffractive
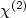medium: variational approach. Optics Comm. 118 (1995) 345–352.
[Google Scholar]
- P.L. Sulem and C. Sulem, The nonlinear Schrödinger equation, Self-focusing and wave collapse. AMS, Springer-Verlag (1999). [Google Scholar]
- I.N. Towers, B.A. Malomed and F.W. Wise, Light bullets in quadratic media with normal dispersion at the second harmonic. Phys. Rev. Lett. 90 (2003) 123902. [CrossRef] [PubMed] [Google Scholar]
- M.I. Weinstein, Nonlinear Schrödinger equations and sharp interpolation estimates. Comm. Math. Phys. 87 (1983) 567–576. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.