EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 43 / No 1 (January-February 2009) ESAIM: M2AN, 43 1 (2009) 139-150 References
Free Access
Issue
ESAIM: M2AN
Volume 43, Number 1, January-February 2009
Page(s) 139 - 150
DOI https://doi.org/10.1051/m2an/2008040
Published online 16 October 2008
  1. F. Alter and V. Caselles, Uniqueness of the Cheeger set of a convex body. Preprint (2007) available at http://cvgmt.sns.it. [Google Scholar]
  2. F. Alter, V. Caselles and A. Chambolle, Evolution of characteristic functions of convex sets in the plane by the minimizing total variation flow. Interfaces Free Bound. 7 (2005) 29–53. [CrossRef] [MathSciNet] [Google Scholar]
  3. L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. Oxford University Press, New York (2000). [Google Scholar]
  4. B. Appleton and H. Talbot, Globally minimal surfaces by continuous maximal flows. IEEE Trans. Pattern Anal. Mach. Intell. 28 (2006) 106–118. [CrossRef] [PubMed] [Google Scholar]
  5. G. Bellettini, V. Caselles, A. Chambolle and M. Novaga, Crystalline mean curvature flow of convex sets. Arch. Ration. Mech. Anal. 179 (2006) 109–152. [CrossRef] [MathSciNet] [Google Scholar]
  6. G. Buttazzo, G. Carlier and M. Comte, On the selection of maximal Cheeger sets. Differential Integral Equations 20 (2007) 991–1004. [MathSciNet] [Google Scholar]
  7. G. Carlier and M. Comte, On a weighted total variation minimization problem. J. Funct. Anal. 250 (2007) 214–226. [CrossRef] [MathSciNet] [Google Scholar]
  8. V. Caselles, A. Chambolle and M. Novaga, Uniqueness of the Cheeger set of a convex body. Pacific J. Math. 232 (2007) 77–90. [CrossRef] [MathSciNet] [Google Scholar]
  9. A. Chambolle, An algorithm for total variation minimization and applications, Special issue on mathematics and image analysis. J. Math. Imaging Vision 20 (2004) 89–97. [CrossRef] [MathSciNet] [Google Scholar]
  10. A. Chambolle and P.-L. Lions, Image recovery via total variation minimization. Numer. Math. 76 (1997) 167–188. [CrossRef] [MathSciNet] [Google Scholar]
  11. P.-L. Combettes, A block-iterative surrogate constraint splitting method for quadratic signal recovery. IEEE Trans. Signal Process. 51 (2003) 1771–1782. [CrossRef] [MathSciNet] [Google Scholar]
  12. P.-L. Combettes and J.-C. Pesquet, image restoration subject to a total variation constraint. IEEE Trans. Image Process. 13 (2004) 1213–1222. [CrossRef] [PubMed] [Google Scholar]
  13. N. Cristescu, A model of stability of slopes in Slope Stability 2000, in Proceedings of Sessions of Geo-Denver 2000, D.V. Griffiths, G.A. Fenton, T.R. Martin Eds., Geotechnical special publication 101 (2000) 86–98. [Google Scholar]
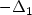  14. F. Demengel, Théorèmes d'existence pour des équations avec l'opérateur “1-Laplacien”, première valeur propre de Formula . C. R. Math. Acad. Sci. Paris 334 (2002) 1071–1076. [CrossRef] [MathSciNet] [Google Scholar]
  15. F. Demengel, Some existence's results for noncoercive “1-Laplacian” operator. Asymptotic Anal. 43 (2005) 287–322. [Google Scholar]
  16. G. Duvaut and J.-L. Lions, Les inéquations en mécanique et en physique. Dunod, Paris (1972). [Google Scholar]
  17. I. Ekeland and R. Temam, Convex Analysis and Variational Problems, Classics in Mathematics. Society for Industrial and Applied Mathematics, Philadelphia (1999). [Google Scholar]
  18. L.C. Evans and R. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press (1992). [Google Scholar]
  19. R. Hassani, I.R. Ionescu and T. Lachand-Robert, Shape optimization and supremal minimization approaches in landslides modeling. Appl. Math. Opt. 52 (2005) 349–364. [CrossRef] [Google Scholar]
  20. P. Hild, I.R. Ionescu, T. Lachand-Robert and I. Rosca, The blocking of an inhomogeneous Bingham fluid. Applications to landslides. ESAIM: M2AN 36 (2002) 1013–1026. [CrossRef] [EDP Sciences] [Google Scholar]
  21. I.R. Ionescu and T. Lachand-Robert, Generalized Cheeger sets related to landslides. Calc. Var. Partial Differential Equations 23 (2005) 227–249. [Google Scholar]
  22. R. Nozawa, Max-flow min-cut theorem in an anisotropic network. Osaka J. Math. 27 (1990) 805–842. [MathSciNet] [Google Scholar]
  23. L.I. Rudin, S. Osher and E. Fatemi, Nonlinear total variation based noise removal algorithms. Physica D 60 (1992) 259–268. [Google Scholar]
  24. G. Strang, Maximal flow through a domain. Math. Programming 26 (1983) 123–143. [CrossRef] [MathSciNet] [Google Scholar]
  25. G. Strang, Maximum flows and minimum cuts in the plane. J. Global Optimization (to appear). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you