| Issue |
ESAIM: M2AN
Volume 33, Number 6, November December 1999
|
|
|---|---|---|
| Page(s) | 1091 - 1120 | |
| DOI | https://doi.org/10.1051/m2an:1999136 | |
| Published online | 15 August 2002 | |
Weak and classical solutions of equations of motion for third grade fluids
Université d'Evry Val d'Essonne, Boulevard des
Coquibus, 91025 Evry Cedex, France.
Received:
23
October
1998
This paper shows that the decomposition method with special
basis, introduced by Cioranescu and Ouazar, allows one to
prove global existence in time of the weak solution for the third
grade fluids, in three dimensions, with small data. Contrary to the
special case where  ,
studied by Amrouche and Cioranescu, the H1 norm of the
velocity is not bounded for all data. This fact, which led others
to think, in contradiction to
this paper, that the method of decomposition could not apply
to the general case of third grade, complicates substantially the
proof of the existence of the solution. We also prove further
regularity results by a method similar to
that of Cioranescu and Girault for second grade fluids. This
extension to the third grade fluids is not straightforward, because of a
transport equation which is much more complex.
,
studied by Amrouche and Cioranescu, the H1 norm of the
velocity is not bounded for all data. This fact, which led others
to think, in contradiction to
this paper, that the method of decomposition could not apply
to the general case of third grade, complicates substantially the
proof of the existence of the solution. We also prove further
regularity results by a method similar to
that of Cioranescu and Girault for second grade fluids. This
extension to the third grade fluids is not straightforward, because of a
transport equation which is much more complex.
Résumé
Dans cet article, on montre que la méthode de décomposition avec
base spéciale introduite par Cioranescu et Ouazar, permet de
démontrer l'existence globale en temps de la solution faible pour les
fluides de grade trois, en dimension trois,
avec des données petites. Contrairement
au cas particulier où 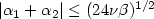 , étudié par
Amrouche et Cioranescu, la norme
H1 de la vitesse n'est pas majorée pour toute donnée. Ce
fait, qui conduisait à penser, en contradiction avec cet
article, que la méthode de décomposition ne pouvait pas s'appliquer
au cas général du grade trois, complique substantiellement la
démonstration d'existence
de la solution. On établit des résultats de régularité par une
méthode similaire à celle de Cioranescu et Girault pour des fluides
, étudié par
Amrouche et Cioranescu, la norme
H1 de la vitesse n'est pas majorée pour toute donnée. Ce
fait, qui conduisait à penser, en contradiction avec cet
article, que la méthode de décomposition ne pouvait pas s'appliquer
au cas général du grade trois, complique substantiellement la
démonstration d'existence
de la solution. On établit des résultats de régularité par une
méthode similaire à celle de Cioranescu et Girault pour des fluides
Mathematics Subject Classification: 35D05 / 35Q99 / 76A05
Key words: Galerkin method / special basis / energy estimates.
© EDP Sciences, SMAI, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


