| Issue |
ESAIM: M2AN
Volume 36, Number 6, November/December 2002
|
|
|---|---|---|
| Page(s) | 1091 - 1109 | |
| DOI | https://doi.org/10.1051/m2an:2003007 | |
| Published online | 15 January 2003 | |
On the two-dimensional compressible isentropic Navier–Stokes equations
Systèmes Physiques de
l'Environnement, UMR CNRS 6134, Université de Corse, Quartier Grossetti, BP 52, 20250 Corte, France. giaco@univ-corse.fr., orenga@univ-corse.fr.
Received:
7
September
2001
Revised:
26
June
2002
We analyze the compressible isentropic Navier–Stokes equations (Lions, 1998) in the two-dimensional case with 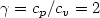 . These equations also modelize
the shallow water problem in height-flow rate formulation used to
solve the flow in lakes and perfectly well-mixed sea. We establish
a convergence result for the time-discretized problem when the
momentum equation and the continuity equation are solved with the
Galerkin method, without adding a penalization term in the
continuity equation as it is made in Lions (1998). The second
part is devoted to the numerical analysis and mainly deals with
problems of geophysical fluids. We compare the simulations
obtained with this compressible isentropic Navier–Stokes model and
those obtained with a shallow water model (Di Martino et al., 1999). At first,
the computations are executed on a simplified domain in order to
validate the method by comparison with existing numerical results
and then on a real domain: the dam of Calacuccia (France).
At last, we numerically implement an analytical
example presented by Weigant (1995) which shows that
even if the data are rather smooth, we cannot have bounds on
ρ in Lp for p large if
. These equations also modelize
the shallow water problem in height-flow rate formulation used to
solve the flow in lakes and perfectly well-mixed sea. We establish
a convergence result for the time-discretized problem when the
momentum equation and the continuity equation are solved with the
Galerkin method, without adding a penalization term in the
continuity equation as it is made in Lions (1998). The second
part is devoted to the numerical analysis and mainly deals with
problems of geophysical fluids. We compare the simulations
obtained with this compressible isentropic Navier–Stokes model and
those obtained with a shallow water model (Di Martino et al., 1999). At first,
the computations are executed on a simplified domain in order to
validate the method by comparison with existing numerical results
and then on a real domain: the dam of Calacuccia (France).
At last, we numerically implement an analytical
example presented by Weigant (1995) which shows that
even if the data are rather smooth, we cannot have bounds on
ρ in Lp for p large if  when N=2.
when N=2.
Mathematics Subject Classification: 35Q30
Key words: Navier–Stokes / compressible / shallow water / time-discretisation / Galerkin.
© EDP Sciences, SMAI, 2002
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


