| Issue |
ESAIM: M2AN
Volume 49, Number 2, March-April 2015
|
|
|---|---|---|
| Page(s) | 373 - 394 | |
| DOI | https://doi.org/10.1051/m2an/2014037 | |
| Published online | 19 February 2015 | |
Discretized fractional substantial calculus∗
School of Mathematics and Statistics, Gansu Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou University, Lanzhou 730000, P.R. China
chenmh2009@lzu.edu.cn; dengwh@lzu.edu.cn
Received: 5 January 2014
Revised: 15 August 2014
This paper discusses the properties and the numerical discretizations of the fractional substantial integral
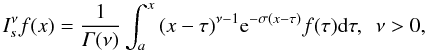and the fractional substantial derivative
where 
, σ can be a constant or a function not related to x, say σ(y); and m is the smallest integer that exceeds μ. The Fourier transform method and fractional linear multistep method are used to analyze the properties or derive the discretized schemes. And the convergences of the presented discretized schemes with the global truncation error 
(p = 1,2,3,4,5) are theoretically proved and numerically verified.
Mathematics Subject Classification: 26A33 / 65L06 / 42A38 / 65M12
Key words: Fractional substantial calculus / fractional linear multistep methods / fourier transform / stability and convergence
© EDP Sciences, SMAI, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.