EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 43 / No 5 (September-October 2009) ESAIM: M2AN, 43 5 (2009) 957-971 References
Free Access
Issue
ESAIM: M2AN
Volume 43, Number 5, September-October 2009
Page(s) 957 - 971
DOI https://doi.org/10.1051/m2an/2009017
Published online 12 June 2009
  1. R. Adams and J.J.F. Fournier, Sobolev Spaces. Academic Press, New York (2003). [Google Scholar]
  2. C. Bi and V. Ginting, Two-grid finite volume element method for linear and nonlinear elliptic problems. Numer. Math. 107 (2007) 177–198. [CrossRef] [Google Scholar]
  3. S.C. Brenner and L.R. Scott, The Mathematical Theory of Finite Element Methods. Springer-Verlag, New York, 2nd edn., (2002). [Google Scholar]
  4. Z. Cai, On the finite volume element method. Numer. Math. 58 (1991) 713–735. [CrossRef] [MathSciNet] [Google Scholar]
  5. Z. Cai, J. Mandel and S. McCormick, The finite volume element method for diffusion equations on general triangulations. SIAM J. Numer. Anal. 28 (1991) 392–402. [CrossRef] [MathSciNet] [Google Scholar]
  6. C. Carstensen, R. Lazarov and S. Tomov, Explicit and averaging a posteriori error estimates for adaptive finite volume methods. SIAM J. Numer. Anal. 42 (2005) 2496–2521. [CrossRef] [MathSciNet] [Google Scholar]
  7. P. Chatzipantelidis and R.D. Lazarov, Error estimates for a finite volume element method for elliptic PDEs in nonconvex polygonal domains. SIAM J. Numer. Anal. 42 (2004) 1932–1958. [CrossRef] [Google Scholar]
  8. P. Chatzipantelidis, R.D. Lazarov and V. Thomée, Error estimates for a finite volume element method for parabolic equations in convex polygonal domains. Numer. Meth. PDEs 20 (2004) 650–674. [Google Scholar]
  9. S.H. Chou and D.Y. Kwak, Multigrid algorithms for a vertex-centered covolume method for elliptic problems. Numer. Math. 90 (2002) 459–486. [CrossRef] [MathSciNet] [Google Scholar]
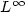  10. S.H. Chou and Q. Li, Error estimates in L2, H1 and Formula in covolume methods for elliptic and parabolic problems: a unified approach. Math. Comp. 69 (2000) 103–120. [Google Scholar]
  11. S.H. Chou, D.Y. Kwak and Q. Li, Lp error estimates and superconvergence for covolume or finite volume element methods. Numer. Meth. PDEs 19 (2003) 463–486. [Google Scholar]
  12. P.G. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978). [Google Scholar]
  13. C.N. Dawson, M.F. Wheeler and C.S. Woodward, A two-grid finite difference scheme for nonlinear parabolic equations. SIAM J. Numer. Anal. 35 (1998) 435–452. [CrossRef] [MathSciNet] [Google Scholar]
  14. J. de Frutos and J. Novo, Postprocessing the linear finite element method. SIAM J. Numer. Anal. 40 (2002) 805–819. [CrossRef] [MathSciNet] [Google Scholar]
  15. R.E. Ewing, T. Lin and Y. Lin, On the accuracy of the finite volume element method based on piecewise linear polynomials. SIAM J. Numer. Anal. 39 (2002) 1865–1888. [Google Scholar]
  16. R. Eymard, T. Gallouët and R. Herbin, Finite Volume Methods: Handbook of Numerical Analysis. North-Holland, Amsterdam (2000). [Google Scholar]
  17. M. Feistauer, J. Felcman, M. Lukáčová-Medvidová and G. Warnecke, Error estimates of a combined finite volume-finite element method for nonlinear convection-diffusion problems. SIAM J. Numer. Anal. 36 (1999) 1528–1548. [CrossRef] [MathSciNet] [Google Scholar]
  18. B. García-Archilla, J. Novo and E.S. Titi, Postprocessing the Galerkin method: a novel approach to approximate inertial manifolds. SIAM J. Numer. Anal. 35 (1998) 941–972. [CrossRef] [MathSciNet] [Google Scholar]
  19. B. García-Archilla and E.S. Titi, Postprocessing the Galerkin method: the finite element case. SIAM J. Numer. Anal. 37 (2000) 470–499. [CrossRef] [MathSciNet] [Google Scholar]
  20. D. Henry, Geometric theory of semilinear parabolic equations, Lecture Notes in Mathematics 840. Springer-Verlag, New York (1989). [Google Scholar]
  21. A. Lasis and E. Süli, hp-version discontinuous Galerkin finite element method for semilinear parabolic problems. SIAM J. Numer. Anal. 45 (2007) 1544–1569. [CrossRef] [MathSciNet] [Google Scholar]
  22. R. Li, Z. Chen and W. Wu, Generalized Difference Methods for Differential Equations: Numerical Analysis of Finite Volume Methods. Marcel Dekker, New York (2000). [Google Scholar]
  23. X. Ma, S. Shu and A. Zhou, Symmetric finite volume discretizations for parabolic problems. Comput. Methods Appl. Mech. Engrg. 192 (2003) 4467–4485. [CrossRef] [MathSciNet] [Google Scholar]
  24. M. Marion and J.C. Xu, Error estimates on a new nonlinear Galerkin method based on two-grid finite elements. SIAM J. Numer. Anal. 32 (1995) 1170–1184. [CrossRef] [MathSciNet] [Google Scholar]
  25. H. Rui, Symmetric modified finite volume element methods for self-adjoint elliptic and parabolic problems. J. Comput. Appl. Math. 146 (2002) 373–386. [CrossRef] [MathSciNet] [Google Scholar]
  26. A.H. Schatz, V. Thomée and L. Wahlbin, Maximum norm stability and error estimates in parabolic finite element equations. Comm. Pure Appl. Math. 33 (1980) 265–304. [CrossRef] [MathSciNet] [Google Scholar]
  27. R.K. Sinha and J. Geiser, Error estimates for finite volume element methods for convection-diffusion-reaction equations. Appl. Numer. Math. 57 (2007) 59–72. [CrossRef] [MathSciNet] [Google Scholar]
  28. R. Temam, Infinite Dimensional Dynamical Systems in Mechanics and Physics, Applied Mathematical Sciences 68. Springer-Verlag, Berlin (1988). [Google Scholar]
  29. V. Thomée, Galerkin Finite Element Methods for Parabolic Problems. Springer-Verlag, Berlin (1997). [Google Scholar]
  30. V. Thomée and L. Wahlbin, On Galerkin methods in semilinear parabolic problems. SIAM J. Numer. Anal. 12 (1975) 378–389. [CrossRef] [MathSciNet] [Google Scholar]
  31. Y. Yan, Postprocessing the finite element method for semilinear parabolic problems. SIAM J. Numer. Anal. 44 (2006) 1681–1702. [CrossRef] [MathSciNet] [Google Scholar]
  32. M. Yang, A second-order finite volume element method on quadrilateral meshes for elliptic equations. ESAIM: M2AN 40 (2006) 1053–1067. [CrossRef] [EDP Sciences] [Google Scholar]
  33. X. Ye, A discontinuous finite volume method for the Stokes problems. SIAM J. Numer. Anal. 44 (2006) 183–198. [CrossRef] [MathSciNet] [Google Scholar]
  34. S. Zhang, On domain decomposition algorithms for covolume methods for elliptic problems. Comput. Methods Appl. Mech. Engrg. 196 (2006) 24–32. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you