EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 46 / No 1 (January-February 2012) ESAIM: M2AN, 46 1 (2012) 145-185 References
Free Access
Issue
ESAIM: M2AN
Volume 46, Number 1, January-February 2012
Page(s) 145 - 185
DOI https://doi.org/10.1051/m2an/2011037
Published online 03 October 2011
  1. T.B. Benjamin, Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 29 (1967) 559–592. [CrossRef] [Google Scholar]
  2. T.B. Benjamin, J.L. Bona and J.J. Mahony, Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. Ser. A 272 (1972) 47–78. [Google Scholar]
  3. C. Besse, Schéma de relaxation pour l'équation de Schrödinger non linéaire et les systèmes de Davey et Stewartson. C. R. Acad. Sci. Paris Sér. I Math. 326 (1998) 1427–1432. [CrossRef] [MathSciNet] [Google Scholar]
  4. C. Besse and C.H. Bruneau, Numerical study of elliptic-hyperbolic Davey-Stewartson system: dromions simulation and blow-up. Math. Mod. Methods Appl. Sci. 8 (1998) 1363–1386. [CrossRef] [Google Scholar]
  5. J.L. Bona, M. Chen and J.-C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. I. Derivation and linear theory. J. Nonlinear Sci. 12 (2002) 283–318. [CrossRef] [MathSciNet] [Google Scholar]
  6. J.L. Bona, T. Colin and D. Lannes, Long wave approximations for water waves. Arch. Ration. Mech. Anal. 178 (2005) 373–410. [CrossRef] [MathSciNet] [Google Scholar]
  7. J.L. Bona, D. Lannes and J.-C. Saut, Asymptotic models for internal waves. J. Math. Pures Appl. 89 (2008) 538–566. [CrossRef] [MathSciNet] [Google Scholar]
  8. J. Boussinesq, Théorie de l'intumescence liquide appelée onde solitaire ou de translation se propageant dans un canal rectangulaire. C. R. Acad. Sci. Paris Sér. A-B 72 (1871) 755–759. [Google Scholar]
  9. J. Boussinesq, Théorie des ondes et des remous qui se propagent le long d'un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 17 (1872) 55–108. [Google Scholar]
  10. F. Chazel, On the Korteweg-de Vries approximation for uneven bottoms. Eur. J. Mech. B Fluids 28 (2009) 234–252. [CrossRef] [MathSciNet] [Google Scholar]
  11. W. Choi and R. Camassa, Weakly nonlinear internal waves in a two-fluid system. J. Fluid Mech. 313 (1996) 83–103. [CrossRef] [MathSciNet] [Google Scholar]
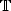  12. J. Colliander, M. Keel, G. Staffilani, H. Takaoka and T. Tao, Sharp global well-posedness for KdV and modified KdV on Formula and Formula . J. Amer. Math. Soc. 16 (2003) 705–749 (electronic). [Google Scholar]
  13. W. Craig, An existence theory for water waves and the Boussinesq and Korteweg-de Vries scaling limits. Commun. Partial Differ. Equ. 10 (1985) 787–1003. [Google Scholar]
  14. W. Craig, P. Guyenne and H. Kalisch, Hamiltonian long-wave expansions for free surfaces and interfaces. Comm. Pure Appl. Math. 58 (2005) 1587–1641. [CrossRef] [MathSciNet] [Google Scholar]
  15. V.D. Djordjevic and L.G. Redekopp, The fission and disintegration of internal solitary waves moving over two-dimensional topography. J. Phys. Oceanogr. 8 (1978) 1016–1024. [CrossRef] [Google Scholar]
  16. V. Duchêne, Asymptotic shallow water models for internal waves in a two-fluid system with a free surface. SIAM J. Math. Anal. 42 (2010) 2229–2260. [CrossRef] [MathSciNet] [Google Scholar]
  17. M. Duruflé and S. Israwi, A numerical study of variable depth KdV equations and generalizations of Camassa-Holm-like equations. Preprint, available at http://hal.archives-ouvertes.fr/hal-00454495/en/. [Google Scholar]
  18. M. Funakoshi and M. Oikawa, Long internal waves of large amplitude in a two-layer fluid. J. Phys. Soc. Japan 55 (1986) 128–144. [CrossRef] [Google Scholar]
  19. R. Grimshaw, E. Pelinovsky and T. Talipova, The modified korteweg-de vries equation in the theory of large-amplitude internal waves. Nonlin. Process. Geophys. 4 (1997) 237–250. [CrossRef] [Google Scholar]
  20. P. Guyenne, Large-amplitude internal solitary waves in a two-fluid model. C. R. Mec. 334 (2006) 341–346. [CrossRef] [Google Scholar]
  21. K.R. Helfrich and W.K. Melville, Long nonlinear internal waves, in Annual review of fluid mechanics 38. Palo Alto, CA (2006) 395–425. [Google Scholar]
  22. T. Kakutani and N. Yamasaki, Solitary waves on a two-layer fluid. J. Phys. Soc. Japan 45 (1978) 674–679. [Google Scholar]
  23. T. Kato and G. Ponce, Commutator estimates and the Euler and Navier-Stokes equations. Comm. Pure Appl. Math. 41 (1988) 891–907. [CrossRef] [MathSciNet] [Google Scholar]
  24. C.E. Kenig, G. Ponce and L. Vega, Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle. Commun. Pure Appl. Math. 46 (1993) 527–620. [CrossRef] [MathSciNet] [Google Scholar]
  25. G.H. Keulegan, Characteristics of internal solitary waves. J. Res. Nat. Bur. Stand 51 (1953) 133–140. [Google Scholar]
  26. C.G. Koop and G. Butler, An investigation of internal solitary waves in a two-fluid system. J. Fluid Mech. 112 (1981) 225–251. [CrossRef] [MathSciNet] [Google Scholar]
  27. D.J. Korteweg and G. De Vries, On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 5 (1895) 422–443. [Google Scholar]
  28. D. Lannes, Secular growth estimates for hyperbolic systems. J. Diff. Equ. 190 (2003) 466–503. [CrossRef] [Google Scholar]
  29. D. Lannes, A stability criterion for two-fluid interfaces and applications. preprint arXiv:1005.4565. [Google Scholar]
  30. C. Leone, H. Segur and J.L. Hammack, Viscous decay of long internal solitary waves. Phys. Fluids 25 (1982) 942–944. [CrossRef] [Google Scholar]
  31. R.R. Long, Long waves in a two-fluid system. J. Meteorol. 13 (1956) 70–74. [CrossRef] [MathSciNet] [Google Scholar]
  32. Y. Matsuno, A unified theory of nonlinear wave propagation in two-layer fluid systems. J. Phys. Soc. Japan 62 (1993) 1902–1916. [CrossRef] [Google Scholar]
  33. H. Michallet and E. Barthélemy, Ultrasonic probes and data processing to study interfacial solitary waves. Exp. Fluids 22 (1997) 380–386. [CrossRef] [Google Scholar]
  34. H. Michallet and E. Barthélemy, Experimental study of interfacial solitary waves. J. Fluid Mech. 366 (1998) 159–177. [CrossRef] [Google Scholar]
  35. H. Ono, Algebraic solitary waves in stratified fluids. J. Phys. Soc. Japan 39 (1975) 1082–1091. [Google Scholar]
  36. L.A. Ostrovsky and Y.A. Stepanyants, Internal solitons in laboratory experiments: comparison with theoretical models. Chaos 15 (2005) 1–28. [CrossRef] [Google Scholar]
  37. T. Sakai and L.G. Redekopp, Models for strongly-nonlinear evolution of long internal waves in a two-layer stratification. Nonlin. Process. Geophys. 14 (2007) 31–47. [CrossRef] [Google Scholar]
  38. G. Schneider and C.E. Wayne, The long-wave limit for the water wave problem. I. The case of zero surface tension. Commun. Pure Appl. Math. 53 (2000) 1475–1535. [Google Scholar]
  39. H. Segur and J.L. Hammack, Soliton models of long internal waves. J. Fluid Mech. 118 (1982) 285–304. [CrossRef] [MathSciNet] [Google Scholar]
  40. M.E. Taylor, Partial differential equations, III Nonlinear equations, Applied Mathematical Sciences 117. Springer-Verlag, New York (1997). [Google Scholar]
  41. L.R. Walker, Interfacial solitary waves in a two-fluid medium. Phys. Fluids 16 (1973) 1796–1804. [CrossRef] [Google Scholar]
  42. V.E. Zakharov, Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (1968) 190–194. [CrossRef] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you