EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 49 / No 3 (May-June 2015) ESAIM: M2AN, 49 3 (2015) 713-740 References
Free Access
Issue
ESAIM: M2AN
Volume 49, Number 3, May-June 2015
Page(s) 713 - 740
DOI https://doi.org/10.1051/m2an/2014043
Published online 08 April 2015
  1. R.A. Adams and J.F. Fournier, Sobolev Spaces. In vol. 140 of Pure and Appl. Math. Ser., 2dn edn. Academic Press (2003). [Google Scholar]
  2. S.C. Brenner, Lower bounds for two-level additive Schwarz preconditioners with small overlaps. SIAM J. Sci. Comput. 21 (2000) 1657–1669. [CrossRef] [Google Scholar]
  3. X.-C. Cai, An additive Schwarz algorithm for nonselfadjoint elliptic equations. In Proc. of Third International Symposium on Domain Decomposition Methods for Partial Differential Equations. Edited by T. Chan, R. Glowinski, J. Périaux and O. Widlund. SIAM, Philadelphia, PA (1990) 232–244. [Google Scholar]
  4. X.-C. Cai, Additive Schwarz algorithms for parabolic convection-diffusion equations. Numer. Math. 60 (1991) 41–61. [CrossRef] [MathSciNet] [Google Scholar]
  5. X.-C. Cai, Multiplicative Schwarz methods for parabolic problems. SIAM J. Sci Comput. 15 (1994) 587–603. [CrossRef] [Google Scholar]
  6. X.-C. Cai and O. Widlund, Multiplicative Schwarz algorithms for some nonsymmetric and indefinite problems. SIAM J. Numer. Anal. 30 (1993) 936–952. [CrossRef] [MathSciNet] [Google Scholar]
  7. C. Canuto and D. Funaro, The Schwarz algorithm for spectral methods. SIAM J. Numer. Anal. 25 (1988) 24–40. [CrossRef] [Google Scholar]
  8. T.F. Chan and T.P. Mathew, Domain decomposition algorithms. In Acta Numerica. Cambridge University Press (1994) 61–143. [Google Scholar]
  9. T.F. Chan, B.F. Smith and J. Zou, Overlapping Schwarz methods on unstructured meshes using non-matching coarse grids. Numer. Math. 73 (1996) 149–167. [CrossRef] [MathSciNet] [Google Scholar]
  10. T.F. Chan and J. Zou, Additive Schwarz domain decomposition methods for elliptic problems on unstructured meshes. Numer. Algorithms 8 (1994) 329–346. [CrossRef] [Google Scholar]
  11. T.F. Chan and J. Zou, A convergence theory of multilevel additive Schwarz methods on unstructured meshes. Numer. Algorithms 13 (1996) 365–398. [CrossRef] [Google Scholar]
  12. L.C. Cowsar, Dual variable Schwarz methods for mixed finite elements. Technical Report TR93-09. Department of Mathematical Sciences, Rice University (1993). [Google Scholar]
  13. M. Dryja, Additive Schwarz methods for elliptic mortar finite element problems. In Modeling and Optimization of Distributed Parameter Systems with Applications to Engineering. Edited by M.P. Kazimierz Malanowski, Z. Nahorski. IFIP, Chapman & Hall, London (1996) 31–50. [Google Scholar]
  14. M. Dryja and O.B. Widlund, An additive variant of the Schwarz alternating method for the case of many subregions. Technical Report 339, also Ultracomputer Note 131. Department of Computer Science, Courant Institute (1987). [Google Scholar]
  15. M. Dryja and O.B. Widlund, Domain decomposition algorithms with small overlap. SIAM J. Sci.Comput. 15 (1994) 604–620. [Google Scholar]
  16. R.E. Ewing and J. Wang, Analysis of the Schwarz algorithm for mixed finite element methods. RAIRO Math. Model. Numer. Anal. 26 (1992) 739–756. [Google Scholar]
  17. X. Feng and O.A. Karakashian, Two-level additive Schwarz methods for a discontinuous Galerkin approximation of second order elliptic problems. SIAM J. Numer. Anal. 39 (2002) 1343–1365. [Google Scholar]
  18. A. Frommer and D.B. Szyld, Weighted max norms, splittings, and overlapping additive Schwarz iterations. Numer. Math. 83 (1999) 259–278. [CrossRef] [MathSciNet] [Google Scholar]
  19. M.J. Gander, Optimized Schwarz methods. SIAM J. Numer. Anal. 44 (2006) 699–731. [CrossRef] [MathSciNet] [Google Scholar]
  20. M.J. Gander, Schwarz methods over the course of time. Electron. Trans. Numer. Anal. 31 (2008) 228–255. [MathSciNet] [Google Scholar]
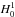  21. M.J. Gander, L. Halpern and K. Santugini-Repiquet, Non shape regular domain decompositions: An analysis using a stable decomposition in Formula . In Domain Decomposition Methods in Science and Engineering XX. Edited by R. Bank, M. Holst, O. Widlund and J. Xu, No. 91. Lect. Notes Comput. Sci. Eng. Springer, Berlin (2013) 485–492. [Google Scholar]
  22. P. Grisvard, Elliptic problems in nonsmooth domains. Pitman Publishing, Boston (1985). [Google Scholar]
  23. M. Arlindo Casarin Jr, Quasi-optimal Schwarz methods for the conforming spectral element discretization. SIAM J. Numer. Anal. 34 (1997) 2482–2502. [CrossRef] [Google Scholar]
  24. P.-L. Lions, On the Schwarz alternating method. I. In First International Symposium on Domain Decomposition Methods for Partial Differential Equations. Edited by R. Glowinski, G.H. Golub, G.A. Meurant and J. Périaux. Philadelphia, PA (1988) 1–42. SIAM. [Google Scholar]
  25. P.-L. Lions, On the Schwarz alternating method. II. In Domain Decomposition Methods. Edited by T. Chan, R. Glowinski, J. Périaux and O. Widlund. SIAM, Philadelphia, PA (1989) 47–70. [Google Scholar]
  26. P.-L. Lions, On the Schwarz alternating method. III: a variant for nonoverlapping subdomains. In Proc. of Third International Symposium on Domain Decomposition Methods for Partial Differential Equations. Edited by T.F. Chan, R. Glowinski, J. Périaux and O. Widlund, held in Houston, Texas, March 20-22, 1989. SIAM, Philadelphia, PA (1990) 202–223. [Google Scholar]
  27. T.P. Mathew, Schwarz alternating and iterative refinement methods for mixed formulations of elliptic problems, part I: Algorithms and numerical results. Numer. Math. 65 (1993) 445–468. [CrossRef] [MathSciNet] [Google Scholar]
  28. T.P. Mathew, Schwarz alternating and iterative refinement methods for mixed formulations of elliptic problems, part II: Theory. Numer. Math. 65 (1993) 469–492. [CrossRef] [MathSciNet] [Google Scholar]
  29. L.F. Pavarino, Additive Schwarz methods for the p-version finite element method. Numer. Math. 66 (1994) 493–515. [CrossRef] [MathSciNet] [Google Scholar]
  30. L.F. Pavarino, Schwarz methods with local refinement for the p-version finite element method. Numer. Math. 69 (1994) 185–211. [CrossRef] [MathSciNet] [Google Scholar]
  31. A. Quarteroni and A. Valli, Domain Decomposition Methods for Partial Differential Equations. Oxford Science Publications (1999). [Google Scholar]
  32. H.A. Schwarz, Über einen Grenzübergang durch alternierendes Verfahren. Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich 15 (1870) 272–286. [Google Scholar]
  33. B.F. Smith, P.E. Bjørstad and W. Gropp, Domain Decomposition: Parallel Multilevel Methods for Elliptic Partial Differential Equations. Cambridge University Press (1996). [Google Scholar]
  34. R. Temam, Infinite Dimensional Dynamical Systems, vol. 68, 2nd edition. Appl. Math. Sci. Springer Verlag (1997). [Google Scholar]
  35. A. Toselli and O. Widlund, Domain Decomposition Methods – Algorithms and Theory. In vol. 34 of Springer Ser. Comput. Math. Springer (2004). [Google Scholar]
  36. O.B. Widlund, The development of coarse spaces for domain decomposition algorithms. In Domain Decomposition Methods in Science and Engineering XVIII. Edited by M. Bercovier, M.J. Gander, R. Kornhuber and O. Widlund. In vol. 70 of Lect. Notes Comput. Sci. Eng. (2009) 241–248. [Google Scholar]
  37. J. Xu, Iterative methods by space decomposition and subspace correction. SIAM Reviews 34 (1992) 581–613. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you