EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 49 / No 4 (July-August 2015) ESAIM: M2AN, 49 4 (2015) 921-951 References
Free Access
Issue
ESAIM: M2AN
Volume 49, Number 4, July-August 2015
Page(s) 921 - 951
DOI https://doi.org/10.1051/m2an/2014060
Published online 19 May 2015
  1. G. Allaire, Conception optimale de structures. Springer-Verlag (2007). [Google Scholar]
  2. P.F. Antonietti, A. Borzì and M. Verani, Multigrid shape optimization governed by elliptic PDEs. SIAM J. Control Optim. 51 (2013) 1417–1440. [CrossRef] [MathSciNet] [Google Scholar]
  3. F. Ballarin, A. Manzoni, G. Rozza and S. Salsa, Shape Optimization by Free-Form Deformation: Existence Results and Numerical Solution for Stokes Flows. J. Sci. Comput. 60 (2013) 537–563. [Google Scholar]
  4. D. Begis and R. Glowinski, Application de la méthode des éléments finis à l’approximation d’un problème de domaine optimal. Méthodes de résolution des problèmes approchés. Appl. Math. Optim. 2 (1975) 130–169. [CrossRef] [MathSciNet] [Google Scholar]
  5. F. Bélahcène and J.A. Desideri, Paramétrisation de Bézier adaptative pour l’optimisation de forme en Aérodynamique. Research Report RR-4943, INRIA (2003). [Google Scholar]
  6. J.A. Bello, E. Fernández-Cara, J. Lemoine and J. Simon, The Differentiability of the Drag with Respect to the Variations of a Lipschitz Domain in a Navier–Stokes Flow. SIAM J. Control Optim. 35 (1997) 626–640. [CrossRef] [MathSciNet] [Google Scholar]
  7. S.C. Brenner and R. Scott, The mathematical theory of finite element methods. Springer Texts Appl. Math., 3rd edition (2008). [Google Scholar]
  8. F. Brezzi, On the existence uniqueness and approximation of saddle point problems arising from lagrangian multipliers. Rev. Fr. Automat. Infor. 8 (1974) 129–151. [Google Scholar]
  9. D. Chenais and E. Zuazua, Controllability of an elliptic equation and its finite difference approximation by the shape of the domain. Numer. Math. 95 (2003) 63–99. [CrossRef] [MathSciNet] [Google Scholar]
  10. D. Chenais and E. Zuazua, Finite-element approximation of 2D elliptic optimal design. J. Math. Pure Appl. 85 (2006) 225–249. [CrossRef] [Google Scholar]
  11. F. de Gournay, G. Allaire and F. Jouve, Shape and topology optimization of the robust compliance via the level set method. ESAIM: COCV 14 (2008) 43–70. [Google Scholar]
  12. M.C. Delfour and J.P. Zolésio, Shapes and geometries. Society for Industrial and Applied Mathematics (SIAM), 2nd edition (2011). [Google Scholar]
  13. G. Dogan, P. Morin, R.H. Nochetto and M. Verani, Discrete gradient flows for shape optimization and applications. Comput. Methods Appl. Mech. 196 (2007) 3898–3914. [Google Scholar]
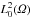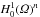  14. R.G. Durán, An elementary proof of the continuity from Formula to Formula of Bogovskii’s right inverse of the divergence. Rev. Un. Mat. Argentina 53 (2013) 59–78. [Google Scholar]
  15. K. Eppler, Second derivatives and sufficient optimality conditions for shape functionals. Control Cybern. 29 (2000) 485–511. [Google Scholar]
  16. K. Eppler, H. Harbrecht and R. Schneider, On Convergence in Elliptic Shape Optimization. SIAM J. Control Optim. 46 (2007) 61–83. [CrossRef] [MathSciNet] [Google Scholar]
  17. I. Fumagalli, Shape optimization for Stokes flows: a reference-domain approach. M.Sc. thesis, Politecnico di Milano, Italy (2013). Available at http://www.mate.polimi.it/biblioteca/?pp=view&id=537&collezione=tesi&L=i. [Google Scholar]
  18. V. Girault and P.A. Raviart, Finite element methods for Navier-Stokes equations. Springer-Verlag (1986). [Google Scholar]
  19. M.D. Gunzburger, Perspectives in flow control and optimization. Society for Industrial and Applied Mathematics (SIAM) (2003). [Google Scholar]
  20. M.D. Gunzburger, H. Kim and S. Manservisi, On a shape control problem for the stationary Navier–Stokes equations. ESAIM: M2AN 34 (2000) 1233–1258. [CrossRef] [EDP Sciences] [Google Scholar]
  21. B. Guo and C. Schwab, Analytic regularity of Stokes flow on polygonal domains in countably weighted Sobolev spaces. J. Comput. Appl. Math. 190 (2006) 487–519. [CrossRef] [MathSciNet] [Google Scholar]
  22. J. Haslinger and R.A.E. Mäkinen, Introduction to shape optimization. Society for Industrial and Applied Mathematics (SIAM) (2003). [Google Scholar]
  23. J. Haslinger and P. Neittaanmäki, Finite element approximation for optimal shape design: Theory and applications. Wiley Chichester (1988). [Google Scholar]
  24. K. Ito and K. Kunisch, Lagrange multiplier approach to variational problems and applications. Society for Industrial and Applied Mathematics (SIAM) (2008). [Google Scholar]
  25. A.M. Khludnev and J. Sokolowski, Modelling and control in solid mechanics. Birkhäuser Verlag, Basel (1997). [Google Scholar]
  26. B. Kiniger and B. Vexler, A priori error estimates for finite element discretizations of a shape optimization problem. ESAIM: M2AN 47 (2013) 1733–1763. [CrossRef] [EDP Sciences] [Google Scholar]
  27. M. Laumen, Newton’s method for a class of optimal shape design problems. SIAM J. Optim. 10 (2000) 503–533. [CrossRef] [Google Scholar]
  28. J.L. Lions, Optimal control of systems governed by partial differential equations. Springer-Verlag (1971). [Google Scholar]
  29. A. Logg, K.A. Mardal and G.N. Wells, Automated Solution of Differential Equations by the Finite Element Method. Springer (2012). [Google Scholar]
  30. P. Morin, R.H. Nochetto, M.S. Pauletti and M. Verani, Adaptive finite element method for shape optimization. ESAIM: COCV 18 (2012) 1122–1149. [CrossRef] [EDP Sciences] [Google Scholar]
  31. J. Nocedal and S.J. Wright, Numerical optimization. 2nd edition, Springer (2006). [Google Scholar]
  32. O. Pironneau, On optimum profiles in Stokes flow. J. Fluid Mech. 59 (1973) 117–128. [Google Scholar]
  33. P. Plotnikov and J. Sokołowski, Compressible Navier-Stokes equations. Theory and shape optimization. Birkhäuser/Springer, Basel (2012). [Google Scholar]
  34. A. Quarteroni and A. Valli, Numerical Approximation of Partial Differential Equations. Series Comput. Math. Springer (2008). [Google Scholar]
  35. J. Sokolowsky and J.P. Zolésio, Introduction to Shape Optimization. Springer-Verlag (1992). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you