Sparse finite element approximation of high-dimensional transport-dominated diffusion problems

Christoph Schwab; Endre Süli; Radu Alexandru Todor

doi:10.1051/m2an:2008027

All issues

Volume 42 / No 5 (September-October 2008)

ESAIM: M2AN, 42 5 (2008) 777-819

Abstract

Free Access

Issue		ESAIM: M2AN Volume 42, Number 5, September-October 2008


Page(s)		777 - 819
DOI		https://doi.org/10.1051/m2an:2008027
Published online		30 July 2008

ESAIM: M2AN 42 (2008) 777-819

Sparse finite element approximation of high-dimensional transport-dominated diffusion problems

Christoph Schwab¹, Endre Süli² and Radu Alexandru Todor¹

¹ Seminar für Angewandte Mathematik, Eidgenössische Technische Hochschule, 8092 Zürich, Switzerland. schwab@sam.math.ethz.ch; todor@math.ethz.ch
² University of Oxford, Computing Laboratory, Wolfson Building, Parks Road, Oxford OX1 3QD, UK. endre.suli@comlab.ox.ac.uk

Received: 7 March 2007

Abstract

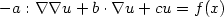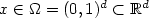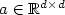We develop the analysis of stabilized sparse tensor-product finite element methods for high-dimensional, non-self-adjoint and possibly degenerate second-order partial differential equations of the form $-a:\nabla\nabla u + b \cdot \nabla u + cu = f(x)$ , $x \in \Omega = (0,1)^d \subset \mathbb{R}^d$ , where $a \in \mathbb{R}^{d\times d}$ is a symmetric positive semidefinite matrix, using piecewise polynomials of degree p ≥ 1. Our convergence analysis is based on new high-dimensional approximation results in sparse tensor-product spaces. 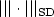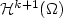We show that the error between the analytical solution u and its stabilized sparse finite element approximation u_h on a partition of Ω of mesh size h = h_L = 2^-L satisfies the following bound in the streamline-diffusion norm $|||\cdot|||_{\rm SD}$ , provided u belongs to the space $\mathcal{H}^{k+1}(\Omega)$ of functions with square-integrable mixed (k+1)st derivatives: $|||u-u_h|||_{\rm SD}\leq C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\} (|\sqrt{a}| h_L^t + |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}} + c^{\frac{1}{2}} h_L^{t+1} \!)|u|_{\mathcal{H}^{t+1}(\Omega)}, \qquad \qquad \qquad$ where $\kappa_i=\kappa_i(p,t,L)$ , i=0,1, and $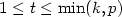1 \leq t \leq \min(k,p)$ . 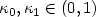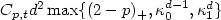We show, under various mild conditions relating L to p, L to d, or p to d, that in the case of elliptic transport-dominated diffusion problems $\kappa_0, \kappa_1 \in (0,1)$ , and hence for p ≥ 1 the 'error constant' $C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\}$ exhibits exponential decay as d → ∞; in the case of a general symmetric positive semidefinite matrix a, the error constant is shown to grow no faster than $\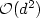mathcal{O}(d^2)$ . 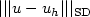In any case, in the absence of assumptions that relate L, p and d, the error $|||u - u_h|||_{\rm SD}$ is still bounded by 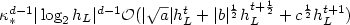$\kappa_\ast^{d-1} |\log_2 h_L|^{d-1}\mathcal{O}(|\sqrt{a}| h_L^t + |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}} + c^{\frac{1}{2}} h_L^{t+1})$ , where 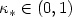$\kappa_\ast \in (0,1)$ for all L, p, d ≥ 2.

Mathematics Subject Classification: 65N30

Key words: High-dimensional Fokker-Planck equations / partial differential equations with nonnegative characteristic form / sparse finite element method.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Sparse finite element approximation of high-dimensional transport-dominated diffusion problems

Recommended for you