| Issue |
ESAIM: M2AN
Volume 33, Number 3, May June 1999
|
|
|---|---|---|
| Page(s) | 517 - 530 | |
| DOI | https://doi.org/10.1051/m2an:1999150 | |
| Published online | 15 August 2002 | |
Non-Trapping sets and Huygens Principle
Dipartimento di Matematica, Università di Roma
“La Sapienza”, Piazzale Aldo Moro 2,
00185 Roma, Italy.
Received:
18
February
1998
Revised:
17
July
1998
We consider the evolution of a set 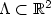 according to the
Huygens principle: i.e. the domain at time t>0, Λt,
is the set of
the points whose distance from Λ is lower than
t. We give some general results for this evolution,
with particular care given to the behavior of the perimeter of the
evoluted set as a function of time.
We define
a class of sets (non-trapping sets) for which the perimeter is a
continuous function of t, and
we give an algorithm to approximate the evolution.
Finally we restrict our attention to the class of sets for which the
turning angle of the boundary is greater than -π (see [2]).
For this class of sets we prove that the perimeter is a
Lipschitz-continuous function of t.
This evolution problem is relevant for the applications
because it is used as a model for solid fuel combustion.
according to the
Huygens principle: i.e. the domain at time t>0, Λt,
is the set of
the points whose distance from Λ is lower than
t. We give some general results for this evolution,
with particular care given to the behavior of the perimeter of the
evoluted set as a function of time.
We define
a class of sets (non-trapping sets) for which the perimeter is a
continuous function of t, and
we give an algorithm to approximate the evolution.
Finally we restrict our attention to the class of sets for which the
turning angle of the boundary is greater than -π (see [2]).
For this class of sets we prove that the perimeter is a
Lipschitz-continuous function of t.
This evolution problem is relevant for the applications
because it is used as a model for solid fuel combustion.
Résumé
Considérons l'évolution d'un ensemble 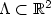 suivant le principe de Huygens : au temps t>0, cet ensemble est
transformé en Λt, l'ensemble des points dont la distance
à Λ est inférieure à t. Nous prouvons quelques
résultats généraux pour cette évolution et nous étudions
en détail l'évolution du périmètre de Λt. Nous
définissons une classe d'ensembles (dits ensembles non-piégeants)
pour lesquels le périmètre est une fonction continue de t,
et nous donnons un algorithme pour approcher cette solution.
Enfin, nous considérons la classe des ensembles pour lesquels
l'intégrale de la courbure sur tout sous-arc orienté de la
frontière est supérieure à -π (voir [2]). Pour cette
classe d'ensembles, nous montrons que le périmètre est une fonction
lipschitzienne de t. Cette évolution du périmètre est
utilisée comme modèle de combustion de propergols solides.
suivant le principe de Huygens : au temps t>0, cet ensemble est
transformé en Λt, l'ensemble des points dont la distance
à Λ est inférieure à t. Nous prouvons quelques
résultats généraux pour cette évolution et nous étudions
en détail l'évolution du périmètre de Λt. Nous
définissons une classe d'ensembles (dits ensembles non-piégeants)
pour lesquels le périmètre est une fonction continue de t,
et nous donnons un algorithme pour approcher cette solution.
Enfin, nous considérons la classe des ensembles pour lesquels
l'intégrale de la courbure sur tout sous-arc orienté de la
frontière est supérieure à -π (voir [2]). Pour cette
classe d'ensembles, nous montrons que le périmètre est une fonction
lipschitzienne de t. Cette évolution du périmètre est
utilisée comme modèle de combustion de propergols solides.
Mathematics Subject Classification: 35Fxx / 49Lxx
Key words: Eikonal equation / distance function.
© EDP Sciences, SMAI, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


