| Issue |
ESAIM: M2AN
Volume 33, Number 3, May June 1999
|
|
|---|---|---|
| Page(s) | 531 - 546 | |
| DOI | https://doi.org/10.1051/m2an:1999151 | |
| Published online | 15 August 2002 | |
L∞(L2) and L∞(L∞) error estimates for mixed methods for integro-differential equations of parabolic type
p
Department of Mathematics, Shandong Normal University,
Jinan, Shandong 250014, People's Republic of China.
Received:
14
May
1997
Revised:
5
August
1998
Error estimates in L∞(0,T;L2(Ω)), L∞(0,T;L2(Ω)2), L∞(0,T;L∞(Ω)), L∞(0,T;
L∞(Ω)2), Ω in 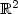 , are derived for a mixed finite
element method for the initial-boundary value problem for integro-differential
equation
, are derived for a mixed finite
element method for the initial-boundary value problem for integro-differential
equation
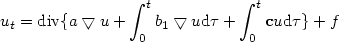 based on the Raviart-Thomas space Vh x Wh ⊂ H(div;Ω) x L2(Ω). Optimal order estimates are obtained for the
approximation of u,ut in L∞(0,T;L2(Ω)) and the
associated velocity p in L∞(0,T;
L2(Ω)2), divp in L∞(0,T;L2(Ω)). Quasi-optimal order estimates are obtained
for the approximation of u in L∞
(0,T;L∞(Ω)) and
p in L∞(0,T;L∞(Ω)2.
based on the Raviart-Thomas space Vh x Wh ⊂ H(div;Ω) x L2(Ω). Optimal order estimates are obtained for the
approximation of u,ut in L∞(0,T;L2(Ω)) and the
associated velocity p in L∞(0,T;
L2(Ω)2), divp in L∞(0,T;L2(Ω)). Quasi-optimal order estimates are obtained
for the approximation of u in L∞
(0,T;L∞(Ω)) and
p in L∞(0,T;L∞(Ω)2.
Résumé
Les estimations d'erreur dans ,
L∞(0,T;L2(Ω)2, L∞(0,T;L∞(Ω)) et L∞(0,T;L∞(Ω)2) avec Ω sous espace de
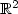 , sont obtenues par une méthode mixte d'éléments finis à partir de la valeur initiale
du problème sur la frontière de l'équation intégro-differentielle:
, sont obtenues par une méthode mixte d'éléments finis à partir de la valeur initiale
du problème sur la frontière de l'équation intégro-differentielle:
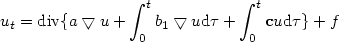 basée sur l'espace de Raviart-Thomas Vn x Wh ⊂ H(div;Ω) x L2(Ω). Les estimations d'ordre optimal sont obtenues à partir de l'approximation de
u, ut dans
L∞(0,T;L2(Ω)), la vitesse associée p dans L∞(0,T;L2(Ω)2, divp
dans L∞(0,T;L2(Ω)). Les estimations d'ordre quasi-optimal sont obtenues à partir de l'approximation de
u dans L∞(0,T;L2(Ω)) et de p dans L∞(0,T;L∞(Ω)2).
basée sur l'espace de Raviart-Thomas Vn x Wh ⊂ H(div;Ω) x L2(Ω). Les estimations d'ordre optimal sont obtenues à partir de l'approximation de
u, ut dans
L∞(0,T;L2(Ω)), la vitesse associée p dans L∞(0,T;L2(Ω)2, divp
dans L∞(0,T;L2(Ω)). Les estimations d'ordre quasi-optimal sont obtenues à partir de l'approximation de
u dans L∞(0,T;L2(Ω)) et de p dans L∞(0,T;L∞(Ω)2).
Mathematics Subject Classification: 35k15 / 35k20 / 45k05
Key words: Error estimates / mixed finite element / integro-differential equations / parabolic type.
© EDP Sciences, SMAI, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


