EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 53 / No 3 (May-June 2019) ESAIM: M2AN, 53 3 (2019) 805-832 References
Open Access
Issue
ESAIM: M2AN
Volume 53, Number 3, May-June 2019
Page(s) 805 - 832
DOI https://doi.org/10.1051/m2an/2018075
Published online 12 June 2019
  1. M. Alfaro and P. Alifrangis, Convergence of a mass conserving Allen-Cahn equation whose lagrange multiplier is nonlocal and local. Interfaces Free Bound. 16 (2014) 243–268. [CrossRef] [Google Scholar]
  2. S.M. Allen and J.W. Cahn, A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27 (1979) 1085–1095. [CrossRef] [Google Scholar]
  3. L. Ambrosio and N. Dancer, Geometric evolution problems, distance function and viscosity solutions. In: Calculus of Variations and Partial Differential Equations (Pisa, 1996), Springer, Berlin (2000) 5–93. [CrossRef] [Google Scholar]
  4. L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press, Oxford (2000). [Google Scholar]
  5. S. Baldo, Minimal interface criterion for phase transitions in mixtures of Cahn-Hilliard fluids. Annales de l’institut. Henri Poincaré (C) Analyse non linéaire 7 (1990) 67–90. [CrossRef] [Google Scholar]
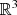  6. J.W. Barrett, H. Garcke and R. Nürnberg, On the parametric finite element approximation of evolving hypersurfaces in Formula . J. Comput. Phys. 227 (2008) 4281–4307. [Google Scholar]
  7. J.W. Barrett, H. Garcke and R. Nürnberg, Parametric approximation of surface clusters driven by isotropic and anisotropic surface energies. Interfaces Free Bound. 12 (2010) 187–234. [CrossRef] [Google Scholar]
  8. P.W. Bates, S. Brown and J.L. Han, Numerical analysis for a nonlocal Allen-Cahn equation. Int. J. Numer. Anal. Model. 6 (2009) 33–49. [Google Scholar]
  9. G. Bellettini and M. Paolini, Quasi-optimal error estimates for the mean curvature flow with a forcing term. Differ. Integral Equ. 8 (1995) 735–752. [Google Scholar]
  10. J. Bence, B. Merriman and S. Osher, Diffusion generated motion by mean curvature, edited by J. Taylor. Computational Crystal Growers Workshop, Selected Lectures in Math. Amer. Math. Soc. (1992) 73–83. [Google Scholar]
  11. K.A. Brakke, The surface evolver. Exp. Math. 1 (1992) 141–165. [Google Scholar]
  12. M. Brassel and E. Bretin, A modified phase field approximation for mean curvature flow with conservation of the volume. Math. Methods Appl. Sci. 34 (2011) 1157–1180. [Google Scholar]
  13. E. Bretin and S. Masnou, A new phase field model for inhomogeneous minimal partitions, and applications to droplets dynamics. Interfaces Free Bound. 19 (2017) 141–182. [CrossRef] [Google Scholar]
  14. G. Caginalp and P.C. Fife, Dynamics of layered interfaces arising from phase boundaries. SIAM J. Appl. Math. 48 (1988) 506–518. [Google Scholar]
  15. J.W. Cahn and J.E. Hilliard, Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (1958) 258–267. [Google Scholar]
  16. X. Chen, Generation and propagation of interfaces for reaction-diffusion equations. J. Differ. Equ. 96 (1992) 116–141. [Google Scholar]
  17. L.Q. Chen and J. Shen, Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 108 (1998) 147–158. [Google Scholar]
  18. Y.G. Chen, Y. Giga and S. Goto, Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations. Proc. Jpn. Acad. Ser. A Math. Sci. 65 (1989) 207–210. [CrossRef] [Google Scholar]
  19. X.F. Chen, C.M. Elliott, A. Gardiner and J.J. Zhao, Convergence of numerical solutions to the Allen-Cahn equation. Appl. Anal. 69 (1998) 47–56. [Google Scholar]
  20. S.J. Cox, F. Graner, F. Vaz, C. Monnereau-Pittet and N. Pittet, Minimal perimeter for n identical bubbles in two dimensions: calculations and simulations. Philos. Mag. 83 (2003) 1393–1406. [CrossRef] [Google Scholar]
  21. K. Deckelnick, G. Dziuk and C.M. Elliott, Computation of geometric partial differential equations and mean curvature flow. Acta Numer. 14 (2005) 139–232. [CrossRef] [MathSciNet] [Google Scholar]
  22. P. de Mottoni and M. Schatzman, Geometrical evolution of developed interfaces. Trans. Amer. Math. Soc. 347 (1995) 1533–1589. [CrossRef] [Google Scholar]
  23. S. Esedoglu and F. Otto, Threshold dynamics for networks with arbitrary surface tensions. Commun. Pure Appl. Math. 68 (2015) 808–864. [Google Scholar]
  24. L.C. Evans and J. Spruck, Motion of level sets by mean curvature. I. J. Differ. Geom. 33 (1991) 635–681. [Google Scholar]
  25. D. Eyre, Computational and Mathematical Models of Microstructural Evolution. Material Research Society, Warrendale, PA (1998). [Google Scholar]
  26. X. Feng and A. Prohl, Analysis of a fully discrete finite element method for the phase field model and approximation of its sharp interface limits. Math. Comput. 73 (2004) 541–567. [Google Scholar]
  27. X. Feng and H.-J. Wu, A posteriori error estimates and an adaptive finite element method for the allen–cahn equation and the mean curvature flow. J. Sci. Comput. 24 (2005) 121–146. [Google Scholar]
  28. H. Garcke, B. Nestler and B. Stoth, On anisotropic order parameter models for multi-phase systems and their sharp interface limits. Phys. D Nonlinear Phenom. 115 (1998) 87–108. [CrossRef] [MathSciNet] [Google Scholar]
  29. H. Garcke, B. Nestler and B. Stoth, A multi phase field concept: Numerical simulations of moving phase boundaries and multiple junctions. SIAM J. Appl. Math. 60 (1999) 295–315. [Google Scholar]
  30. D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order. Springer, Berlin (1998). [Google Scholar]
  31. J. Gruber, N. Ma, Y. Wang, A.D. Rollett and G.S. Rohrer, Sparse data structure and algorithm for the phase field method. Model. Simul. Mater. Sci. Eng. 14 (2006) 1189. [CrossRef] [Google Scholar]
  32. C. Herring, Surface Tension as a Motivation for Sintering. Springer, Berlin Heidelberg, Berlin, Heidelberg (1999) 33–69. [Google Scholar]
  33. H. Ishii, G.E. Pires and P.E. Souganidis, Threshold dynamics type approximation schemes for propagating fronts. J. Math. Soc. Jpn. 51 (1999) 267–308. [CrossRef] [Google Scholar]
  34. Y. Li, H.G. Lee, D. Jeong and J. Kim, An unconditionally stable hybrid numerical method for solving the allen–cahn equation. Comput. Math. Appl. 60 (2010) 1591–1606. [Google Scholar]
  35. P. Loreti and R. March, Propagation of fronts in a nonlinear fourth order equation. Eur. J. Appl. Math. 11 (2000) 203–213. [Google Scholar]
  36. F. Maggi, Sets of Finite Perimeter and Geometric Variational Problems: An Introduction to Geometric Measure Theory. Cambridge University Press, Cambridge (2012). [CrossRef] [Google Scholar]
  37. L. Modica and S. Mortola, Un esempio di Γ-convergenza. Boll. Un. Mat. Ital. B (5) 14 (1977) 285–299. [Google Scholar]
  38. F. Morgan, The hexagonal honeycomb conjecture. Trans. Am. Math. Soc. 351 (1999) 1753–1763. [Google Scholar]
  39. W.W. Mullins, Two-Dimensional Motion of Idealized Grain Boundaries. Springer, Berlin Heidelberg, Berlin, Heidelberg (1999) 70–74. [Google Scholar]
  40. R. Nürnberg, Numerical simulations of immiscible fluid clusters. Appl. Numer. Math. 59 (2009) 1612–1628. [Google Scholar]
  41. S. Osher and R. Fedkiw, Level Set Methods and Dynamic Implicit Surfaces. Applied Mathematical Sciences. Springer-Verlag, New York, New York, NY (2002). [Google Scholar]
  42. S. Osher and N. Paragios, Geometric Level Set Methods in Imaging, Vision and Graphics. Springer-Verlag, New York (2003). [Google Scholar]
  43. S. Osher and J.A. Sethian, Fronts propagating with curvature-dependent speed: algorithms based on hamilton-jacobi formulations. J. Comput. Phys. 79 (1988) 12–49. [Google Scholar]
  44. E. Oudet, Approximation of partitions of least perimeter by Gamma-convergence: around Kelvin’s conjecture. Exp. Math. 20 (2011) 260–270. [Google Scholar]
  45. R.L. Pego, Front migration in the nonlinear Cahn-Hilliard equation. Proc. Roy. Soc. London Ser. A 422 (1989) 261–278. [Google Scholar]
  46. S.J. Ruuth, Efficient algorithms for diffusion-generated motion by mean curvature. J. Comput. Phys. 144 (1998) 603–625. [Google Scholar]
  47. J. Shen, C. Wang, X. Wang and S.M. Wise, Second-order convex splitting schemes for gradient flows with ehrlich-schwoebel type energy: Application to thin film epitaxy. SIAM J. Numer. Anal. 50 (2012) 105–125. [Google Scholar]
  48. L. Vanherpe, N. Moelans, B. Blanpain and S. Vandewalle, Bounding box algorithm for three-dimensional phase-field simulations of microstructural evolution in polycrystalline materials. Phys. Rev. E 76 (2007) 056702. [Google Scholar]
  49. S. Vedantam and B.S.V. Patnaik, Efficient numerical algorithm for multiphase field simulations. Phys. Rev. E 73 (2006) 016703. [Google Scholar]
  50. D. Weaire and R. Phelan, A counter-example to kelvin’s conjecture on minimal surfaces. Philos. Mag. Lett. 69 (1994) 107–110. [Google Scholar]
  51. J.H.C. Whitehead, Simplicial spaces, nuclei and m-groups. Proc. London Math. Soc. 2 (1939) 243–327. [CrossRef] [Google Scholar]
  52. J. Zhang and Q. Du, Numerical studies of discrete approximations to the Allen-Cahn equation in the sharp interface limit. SIAM J. Sci. Comput. 31 (2009) 3042–3063. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you