| Issue |
ESAIM: M2AN
Volume 33, Number 1, January Fabruary 1999
|
|
|---|---|---|
| Page(s) | 169 - 189 | |
| DOI | https://doi.org/10.1051/m2an:1999101 | |
| Published online | 15 August 2002 | |
Un résultat de convergence d'ordre deux en temps pour l'approximation des équations de Navier–Stokes par une technique de projection incrémentale
Laboratoire d'Informatique pour la Mécanique
et les Sciences de l'Ingénieur, CNRS, B.P. 133,
91403, Orsay, France. guermond@limsi.fr..
Received:
12
February
1997
Revised:
26
August
1997
The Navier–Stokes equations are approximated by means of
a fractional step, Chorin–Temam projection method; the time derivative
is approximated by a three-level backward finite difference, whereas
the approximation in space is performed by a Galerkin technique.
It is shown that the proposed scheme yields an error
of 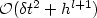 for the velocity in the norm of l2(L2(Ω)d), where l ≥ 1 is
the polynomial degree of the velocity approximation. It is also shown
that the splitting error of projection schemes based on the
incremental pressure correction is of
for the velocity in the norm of l2(L2(Ω)d), where l ≥ 1 is
the polynomial degree of the velocity approximation. It is also shown
that the splitting error of projection schemes based on the
incremental pressure correction is of 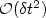 independent of the
approximation order of the velocity time derivative.
independent of the
approximation order of the velocity time derivative.
Résumé
Les équations de Navier–Stokes sont approchées en temps par
une schéma de différentiation rétrograde d'ordre deux et une technique
de pas fractionnaire du type projection de Chorin–Temam ; l'approximation
spatiale est réalisée par une technique de Galerkin. On montre
qu'en temps fini, le schéma est d'ordre 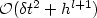 pour la vitesse dans la norme l2(L2(Ω)d), où l ≥ 1 est le
degré polynomial d'approximation de la vitesse. On montre aussi
que l'erreur de fractionnement des schémas de projection basés sur une
correction de pression incrémentale est d'ordre
pour la vitesse dans la norme l2(L2(Ω)d), où l ≥ 1 est le
degré polynomial d'approximation de la vitesse. On montre aussi
que l'erreur de fractionnement des schémas de projection basés sur une
correction de pression incrémentale est d'ordre 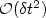 ,
que l'approximation de la dérivée temporelle de la
vitesse soit d'ordre un ou d'ordre deux.
,
que l'approximation de la dérivée temporelle de la
vitesse soit d'ordre un ou d'ordre deux.
Mathematics Subject Classification: 35Q30 / 65M12 / 65M60 / 35Q30 / 65M12 / 65M60
Key words: Incompressible Navier–Stokes equations / Projection method / Second order approximation Fractional-step method / Finite elements. / Incompressible Navier–Stokes equations / Projection method / Second order approximation Fractional-step method / Finite elements.
© EDP Sciences, SMAI, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


