EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 35 / No 5 (September-October 2001) ESAIM: M2AN, 35 5 (2001) 907-920 References
Free Access
Issue
ESAIM: M2AN
Volume 35, Number 5, September-October 2001
Page(s) 907 - 920
DOI https://doi.org/10.1051/m2an:2001142
Published online 15 April 2002
  1. G. Acosta and R.G. Durán, The maximum angle condition for mixed and non-conforming elements, application to the Stokes equations. SIAM J. Numer. Anal. 37 (1999) 18-36. [CrossRef] [MathSciNet] [Google Scholar]
  2. Th. Apel, Anisotropic Finite Elements: Local Estimates and Applications, in Advances in Numerical Mathematics, Teubner, Eds., Stuttgart (1999). [Google Scholar]
  3. Th. Apel and M. Dobrowolski, Anisotropic interpolation with applications to the finite element method. Computing 47 (1992) 277-293. [CrossRef] [MathSciNet] [Google Scholar]
  4. Th. Apel and S. Nicaise, Elliptic problems in domains with edges: anisotropic regularity and anisotropic finite element meshes, in Partial Differential Equations and Functional Analysis (in memory of Pierre Grisvard), J. Céa, D. Chenais, G. Geymonat, and J.-L. Lions, Eds., Birkhäuser, Boston (1996) 18-34. [Google Scholar]
  5. Th. Apel and S. Nicaise, The finite element method with anisotropic mesh grading for elliptic problems in domains with corners and edges. Math. Methods Appl. Sci. 21 (1998) 519-549. [CrossRef] [MathSciNet] [Google Scholar]
  6. Th. Apel, S. Nicaise and J. Schöberl, A non-conforming FEM with anisotropic mesh grading for the Stokes problem in domains with edges. To appear in IMAJ Numer. Anal. [Google Scholar]
  7. Th. Apel, A.-M. Sändig, J.R. Whiteman, Graded mesh refinement and error estimates for finite element solutions of elliptic boundary value problems in non-smooth domains. Math. Methods Appl. Sci. 19 (1996) 63-85. [CrossRef] [MathSciNet] [Google Scholar]
  8. I. Babuska and A.K. Aziz, On the angle condition in the finite element method. SIAM J. Numer. Anal. 13 (1976) 214-226. [CrossRef] [MathSciNet] [Google Scholar]
  9. F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods, in Springer Series in Computational Mathematics 15, Springer-Verlag, Berlin (1991). [Google Scholar]
  10. P.G. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland Publishing Company, Amsterdam, New York, Oxford (1978). [Google Scholar]
  11. M. Dauge, Elliptic Boundary Value Problems on Corner Domains, in Lecture Notes in Mathematics 1341, Springer-Verlag, Berlin, Heidelberg, New York (1988). [Google Scholar]
  12. M. Dauge, Stationary Stokes and Navier-Stokes systems on two- or three-dimensional domains with corners I. SIAM J. Math. Anal. 20 (1989) 74-97. [CrossRef] [MathSciNet] [Google Scholar]
  13. M. Farhloul, Mixed and nonconforming finite element methods for the Stokes problem. Can. Appl. Math. Quart. 3 (1995) 399-418. [Google Scholar]
  14. M. Farhloul and M. Fortin, A new mixed finite element for the Stokes and elasticity problems. SIAM J. Numer. Anal. 30 (1993) 971-990. [CrossRef] [MathSciNet] [Google Scholar]
  15. V. Girault and P.-A. Raviart, Finite Element Methods for Navier-Stokes Equations, in Springer Series in Computational Mathematics 5, Springer-Verlag, Berlin, Heidelberg, New York (1986). [Google Scholar]
  16. P. Grisvard, Elliptic Problems in NonSmooth Domains, in Monographs and Studies in Mathematics 24, Pitman, Boston (1985). [Google Scholar]
  17. J. Lubuma and S. Nicaise, Dirichlet problems in polyhedral domains II: Approximation by FEM and BEM. J. Comp. Appl. Math. 61 (1995) 13-27. [Google Scholar]
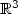  18. J.-C. Nédélec, Mixed finite elements in Formula . Numer. Math. 35 (1980) 315-341. [CrossRef] [MathSciNet] [Google Scholar]
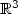  19. J.-C. Nédélec, A new family of mixed finite elements in Formula . Numer. Math. 50 (1986) 57-81. [CrossRef] [MathSciNet] [Google Scholar]
  20. S. Nicaise, Edge elements on anisotropic meshes and approximation of the Maxwell equations. Submitted to SIAM J. Numer. Anal. [Google Scholar]
  21. L.A. Oganesyan and L.A. Rukhovets, Variational-difference methods for the solution of elliptic equations. Izd. Akad. Nauk Armyanskoi SSR, Jerevan (1979). In Russian. [Google Scholar]
  22. G. Raugel, Résolution numérique par une méthode d'éléments finis du problème Dirichlet pour le Laplacien dans un polygone. C. R. Acad. Sci. Paris Sér. A 286 (1978) 791-794. [Google Scholar]
  23. P.A. Raviart and J.M. Thomas, A mixed finite element method for second order elliptic problems, in Mathematical Aspects of Finite Element Methods, in Lecture Notes in Mathematics 606, I. Galligani and E. Magenes, Eds., Springer-Verlag, Berlin (1977) 292-315. [Google Scholar]
  24. J.E. Roberts and J.M. Thomas, Mixed and hybrid methods, in Handbook of Numerical Analysis, Vol. II, Finite Element Methods (Part 1), J.-L. Lions and P.G. Ciarlet, Eds., North-Holland Publishing Company, Amsterdam, New York, Oxford (1991) 523-639. [Google Scholar]
  25. H. El Sossa and L. Paquet, Refined mixed finite element method of the Dirichlet problem for the Laplace equation in a polygonal domain, in Rapport de Recherche 00-5, Laboratoire MACS, Université de Valenciennes, France. Submitted to Adv. Math. Sc. Appl. [Google Scholar]
  26. H. El Sossa and L. Paquet, Méthodes d'éléments finis mixtes raffinés pour le problème de Stokes, in Rapport de Recherche 01-1, Laboratoire MACS, Université de Valenciennes, France. [Google Scholar]
  27. J.M. Thomas, Sur l'analyse numérique des méthodes d'élements finis mixtes et hybrides. Thèse d'État, Université Pierre et Marie Curie, Paris (1977). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you