EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 42 / No 5 (September-October 2008) ESAIM: M2AN, 42 5 (2008) 821-849 References
Free Access
Issue
ESAIM: M2AN
Volume 42, Number 5, September-October 2008
Page(s) 821 - 849
DOI https://doi.org/10.1051/m2an:2008025
Published online 04 July 2008
  1. M. Ainsworth and L. Demkowicz, Explicit polynomial preserving trace liftings on a triangle. Math. Nachr. (to appear). [Google Scholar]
  2. M. Ainsworth and D. Kay, The approximation theory for the p-version finite element method and application to non-linear elliptic PDEs. Numer. Math. 82 (1999) 351–388. [CrossRef] [MathSciNet] [Google Scholar]
  3. M. Ainsworth and K. Pinchedez, The hp-MITC finite element method for the Reissner-Mindlin plate problem. J. Comput. Appl. Math. 148 (2002) 429–462. [CrossRef] [MathSciNet] [Google Scholar]
  4. M. Ainsworth, W. McLean and T. Tran, The conditioning of boundary element equations on locally refined meshes and preconditioning by diagonal scaling. SIAM J. Numer. Anal. 36 (1999) 1901–1932. [CrossRef] [MathSciNet] [Google Scholar]
  5. I. Babuška and B.Q. Guo, Optimal estimates for lower and upper bounds of approximation errors in the p-version of the finite element method in two dimensions. Numer. Math. 85 (2000) 219–255. [CrossRef] [MathSciNet] [Google Scholar]
  6. I. Babuška and M. Suri, The h-p version of the finite element method with quasiuniform meshes. RAIRO Modél. Math. Anal. Numér. 21 (1987) 199–238. [MathSciNet] [Google Scholar]
  7. I. Babuška and M. Suri, The optimal convergence rate of the p-version of the finite element method. SIAM J. Numer. Anal. 24 (1987) 750–776. [CrossRef] [MathSciNet] [Google Scholar]
  8. I. Babuška and M. Suri, The treatment of nonhomogeneous Dirichlet boundary conditions by the p-version of the finite element method. Numer. Math. 55 (1989) 97–121. [CrossRef] [MathSciNet] [Google Scholar]
  9. I. Babuška, R.B. Kellogg and J. Pitkäranta, Direct and inverse error estimates for finite elements with mesh refinement. Numer. Math. 33 (1979) 447–471. [CrossRef] [MathSciNet] [Google Scholar]
  10. J. Bergh and J. Löfström, Interpolation Spaces, Grundlehren der mathematischen Wissenschaften 223. Springer-Verlag, Berlin (1976). [Google Scholar]
  11. A. Bespalov and N. Heuer, The p-version of the boundary element method for hypersingular operators on piecewise plane open surfaces. Numer. Math. 100 (2005) 185–209. [CrossRef] [MathSciNet] [Google Scholar]
  12. A. Bespalov and N. Heuer, The p-version of the boundary element method for weakly singular operators on piecewise plane open surfaces. Numer. Math. 106 (2007) 69–97. [CrossRef] [MathSciNet] [Google Scholar]
  13. P.G. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978). [Google Scholar]
  14. M. Costabel, Boundary integral operators on Lipschitz domains: Elementary results. SIAM J. Math. Anal. 19 (1988) 613–626. [CrossRef] [MathSciNet] [Google Scholar]
  15. L. Demkowicz, Polynomial exact sequences and projection-based interpolation with applications to Maxwell equations, in Mixed Finite Elements, Compatibility Conditions and Applications, D. Boffi and L. Gastaldi Eds., Lecture Notes in Mathematics 1939, Springer-Verlag (2008). [Google Scholar]
  16. L. Demkowicz and I. Babuška, p interpolation error estimates for edge finite elements of variable order in two dimensions. SIAM J. Numer. Anal. 41 (2003) 1195–1208. [CrossRef] [MathSciNet] [Google Scholar]
  17. V.J. Ervin and N. Heuer, An adaptive boundary element method for the exterior Stokes problem in three dimensions. IMA J. Numer. Anal. 26 (2006) 297–325. [CrossRef] [MathSciNet] [Google Scholar]
  18. P. Grisvard, Elliptic Problems in Nonsmooth Domains. Pitman Publishing Inc., Boston (1985). [Google Scholar]
  19. B.Q. Guo, Approximation theory for the p-version of the finite element method in three dimensions. Part 1: Approximabilities of singular functions in the framework of the Jacobi-weighted Besov and Sobolev spaces. SIAM J. Numer. Anal. 44 (2006) 246–269. [CrossRef] [MathSciNet] [Google Scholar]
  20. B.Q. Guo and N. Heuer, The optimal rate of convergence of the p-version of the boundary element method in two dimensions. Numer. Math. 98 (2004) 499–538. [MathSciNet] [Google Scholar]
  21. B.Q. Guo and N. Heuer, The optimal convergence of the h-p version of the boundary element method with quasiuniform meshes for elliptic problems on polygonal domains. Adv. Comp. Math. 24 (2006) 353–374. [CrossRef] [Google Scholar]
  22. N. Heuer and F. Leydecker, An extension theorem for polynomials on triangles. Calcolo 45 (2008) 69–85. [CrossRef] [MathSciNet] [Google Scholar]
  23. N. Heuer, M. Maischak and E.P. Stephan, Exponential convergence of the hp-version for the boundary element method on open surfaces. Numer. Math. 83 (1999) 641–666. [MathSciNet] [Google Scholar]
  24. J.-L. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems and Applications I. Springer-Verlag, New York (1972). [Google Scholar]
  25. P. Monk, On the p- and hp-extension of Nédélec's curl-conforming elements. J. Comput. Appl. Math. 53 (1994) 117–137. [CrossRef] [MathSciNet] [Google Scholar]
  26. J. Nečas, Les Méthodes Directes en Théorie des Équations Elliptiques. Academia, Prague (1967). [Google Scholar]
  27. C. Schwab, p- and hp-Finite Element Methods. Clarendon Press, Oxford (1998). [Google Scholar]
  28. C. Schwab and M. Suri, The optimal p-version approximation of singularities on polyhedra in the boundary element method. SIAM J. Numer. Anal. 33 (1996) 729–759. [CrossRef] [MathSciNet] [Google Scholar]
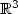  29. E.P. Stephan, Boundary integral equations for screen problems in Formula . Integr. Equ. Oper. Theory 10 (1987) 257–263. [Google Scholar]
  30. E.P. Stephan, The h-p boundary element method for solving 2- and 3-dimensional problems. Comput. Methods Appl. Mech. Engrg. 133 (1996) 183–208. [CrossRef] [MathSciNet] [Google Scholar]
  31. E.P. Stephan and M. Suri, The h-p version of the boundary element method on polygonal domains with quasiuniform meshes. RAIRO Modél. Math. Anal. Numér. 25 (1991) 783–807. [MathSciNet] [Google Scholar]
  32. T. von Petersdorff, Randwertprobleme der Elastizitätstheorie für Polyeder – Singularitäten und Approximation mit Randelementmethoden. Ph.D. thesis, Technische Hochschule Darmstadt, Germany (1989). [Google Scholar]
  33. T. von Petersdorff and E.P. Stephan, Regularity of mixed boundary value problems in 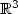Formula and boundary element methods on graded meshes. Math. Methods Appl. Sci. 12 (1990) 229–249. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Recommended for you