Free Access
| Issue |
ESAIM: M2AN
Volume 40, Number 5, September-October 2006
|
|
|---|---|---|
| Page(s) | 871 - 896 | |
| DOI | https://doi.org/10.1051/m2an:2006033 | |
| Published online | 16 January 2007 | |
- D.P. Almond and P.M. Patel, Photothermal science and techniques. Chapman and Hall, London (1996). [Google Scholar]
- J.-P. Aubin, Approximation of elliptic boundary-value problems. Wiley-Interscience, New York-London-Sydney (1972). [Google Scholar]
- H.T. Banks, F. Kojima and W.P. Winfree, Boundary estimation problems arising in thermal tomography. Inverse Problems 6 (1990) 897–921. [Google Scholar]
- F. Brezzi and M. Fortin, Mixed and hybrid finite element methods. Springer-Verlag, New York (1991). [Google Scholar]
- F. Brezzi and C. Johnson, On the coupling of boundary integral and finite element methods. Calcolo 16 (1979) 189–201. [CrossRef] [MathSciNet] [Google Scholar]
- G. Chen and J. Zhou, Boundary element methods. Academic Press, London (1992). [Google Scholar]
- M. Costabel, Symmetric methods for the coupling of finite elements and boundary elements. Boundary elements IX, Vol. 1 (Stuttgart, 1987), Comput. Mech. (1987) 411–420. [Google Scholar]
- M. Costabel and E. Stephan, A direct boundary integral equation method for transmission problems. J. Math. Anal. Appl. 106 (1985) 367–413. [CrossRef] [MathSciNet] [Google Scholar]
- M. Crouzeix and F.-J. Sayas, Asymptotic expansions of the error of spline Galerkin boundary element methods. Numer. Math. 78 (1998) 523–547. [CrossRef] [MathSciNet] [Google Scholar]
- F. Garrido and A. Salazar, Thermal wave scattering by spheres. J. Appl. Phys. 95 (2004) 140–149. [CrossRef] [Google Scholar]
-
G.N. Gatica and G.C. Hsiao, On the coupled BEM and FEM for a nonlinear exterior Dirichlet problem in
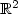 . Numer. Math. 61 (1992) 171–214.
[CrossRef]
[MathSciNet]
[Google Scholar]
. Numer. Math. 61 (1992) 171–214.
[CrossRef]
[MathSciNet]
[Google Scholar]
- G.N. Gatica and G.C. Hsiao, Boundary-field equation methods for a class of nonlinear problems. Pitman Research Notes in Mathematics Series 331, Longman Scientific and Technical, Harlow, UK (1995). [Google Scholar]
- G.N. Gatica and S. Meddahi, A dual-dual mixed formulation for nonlinear exterior transmission problems. Math. Comp. 70 (2001) 1461–1480. [CrossRef] [MathSciNet] [Google Scholar]
- V. Girault and P.-A. Raviart, Finite element methods for Navier-Stokes equations. Theory and algorithms. Springer-Verlag, New York (1986). [Google Scholar]
- H. Han, A new class of variational formulations for the coupling of finite and boundary element methods. J. Comput. Math. 8 (1990) 223–232. [MathSciNet] [Google Scholar]
- T. Hohage, M.-L. Rapún and F.-J. Sayas, Detecting corrosion using thermal measurements. Inverse Probl. (to appear). [Google Scholar]
- G.C. Hsiao, The coupling of BEM and FEM – a brief review. Boundary elements X, Vol 1 (Southampton, 1988). Comput. Mech. (1988) 431–445. [Google Scholar]
- G.C. Hsiao, P. Kopp and W.L. Wendland, A Galerkin collocation method for some integral equations of the first kind. Computing 25 (1980) 89–130. [CrossRef] [MathSciNet] [Google Scholar]
- G.C. Hsiao, P. Kopp and W.L. Wendland, Some applications of a Galerkin-collocation method for boundary integral equations of the first kind. Math. Method. Appl. Sci. 6 (1984) 280–325. [CrossRef] [Google Scholar]
- C. Johnson and J.-C. Nédélec, On the coupling of boundary integral and finite element methods. Math. Comp. 35 (1980) 1063–1079. [CrossRef] [MathSciNet] [Google Scholar]
- R.E. Kleinman and P.A. Martin, On single integral equations for the transmission problem of acoustics. SIAM J. Appl. Math 48 (1988) 307–325. [CrossRef] [MathSciNet] [Google Scholar]
- R. Kress, Linear integral equations. Second edition. Springer-Verlag, New York (1999). [Google Scholar]
- R. Kress and G.F. Roach, Transmission problems for the Helmholtz equation. J. Math. Phys. 19 (1978) 1433–1437. [CrossRef] [Google Scholar]
- M. Lenoir, Optimal isoparametric finite elements and error estimates for domains involving curved boundaries. SIAM J. Num Anal. 23 (1986) 562–580. [Google Scholar]
- A. Mandelis, Photoacoustic and thermal wave phenomena in semiconductors. North-Holland, New York (1987). [Google Scholar]
- A. Mandelis, Diffusion-wave fields. Mathematical methods and Green functions. Springer-Verlag, New York (2001). [Google Scholar]
- A. Márquez, S. Meddahi and V. Selgas, A new BEM-FEM coupling strategy for two-dimensional fluid-solid interaction problems. J. Comput. Phys. 199 (2004) 205–220. [CrossRef] [MathSciNet] [Google Scholar]
- W. McLean, Strongly elliptic systems and boundary integral equations. Cambridge University Press, Cambridge (2000). [Google Scholar]
- S. Meddahi, A mixed-FEM and BEM coupling for a two-dimensional eddy current problem. Numer. Funct. Anal. Optim. 22 (2001) 127–141. [CrossRef] [MathSciNet] [Google Scholar]
- S. Meddahi and A. Márquez, A combination of spectral and finite elements for an exterior problem in the plane. Appl. Numer. Math. 43 (2002) 275–295. [CrossRef] [MathSciNet] [Google Scholar]
- S. Meddahi and F.-J. Sayas, A fully discrete BEM-FEM for the exterior Stokes problem in the plane. SIAM J. Numer. Anal. 37 (2000) 2082–2102. [CrossRef] [MathSciNet] [Google Scholar]
- S. Meddahi and F.-J. Sayas, Analysis of a new BEM-FEM coupling for two-dimensional fluid-solid interaction. Numer. Methods Partial Differ. Equ. 21 (2005) 1017–1042. [CrossRef] [Google Scholar]
- S. Meddahi and V. Selgas, A mixed-FEM and BEM coupling for a three-dimensional eddy current problem. ESAIM: M2AN 37 (2003) 291–318. [CrossRef] [EDP Sciences] [Google Scholar]
- S. Meddahi, J. Valdés, O. Menéndez and P. Pérez, On the coupling of boundary integral and mixed finite element methods. J. Comput. Appl. Math. 69 (1996) 113–124. [CrossRef] [MathSciNet] [Google Scholar]
- S. Meddahi, A. Márquez and V. Selgas, Computing acoustic waves in an inhomogeneous medium of the plane by a coupling of spectral and finite elements. SIAM J. Numer. Anal. 41 (2003) 1729–1750. [CrossRef] [MathSciNet] [Google Scholar]
- S.G. Mikhlin, Mathematical Physics, an advanced course. North-Holland, Amsterdam-London (1970). [Google Scholar]
- L. Nicolaides and A. Mandelis, Image-enhanced thermal-wave slice diffraction tomography with numerically simulated reconstructions. Inverse problems 13 (1997) 1393–1412. [CrossRef] [Google Scholar]
- M.-L. Rapún, Numerical methods for the study of the scattering of thermal waves. Ph.D. Thesis, University of Zaragoza, (2004). In Spanish. [Google Scholar]
- M.-L. Rapún and F.-J. Sayas, Boundary integral approximation of a heat diffusion problem in time-harmonic regime. Numer. Algorithms 41 (2006) 127–160. [CrossRef] [MathSciNet] [Google Scholar]
- F.-J. Sayas, A nodal coupling of finite and boundary elements. Numer. Methods Partial Differ. Equ. 19 (2003) 555–570. [CrossRef] [Google Scholar]
- J.M. Terrón, A. Salazar and A. Sánchez-Lavega, General solution for the thermal wave scattering in fiber composites. J. Appl. Phys. 91 (2002) 1087–1098. [CrossRef] [Google Scholar]
- R.H. Torres and G.V. Welland, The Helmholtz equation and transmission problems with Lipschitz interfaces. Indiana Univ. Math. J. 42 (1993) 1457–1485. [CrossRef] [MathSciNet] [Google Scholar]
- T. von Petersdorff, Boundary integral equations for mixed Dirichlet, Neumann and transmission problems. Math. Methods Appl. Sci. 11 (1989) 185–213. [CrossRef] [MathSciNet] [Google Scholar]
- A. Ženišek, Nonlinear elliptic and evolution problems and their finite element approximations. Academic Press, London (1990). [Google Scholar]
- M. Zlámal, Curved elements in the finite element method I. SIAM J. Numer. Anal. 10 (1973) 229–240. [CrossRef] [MathSciNet] [Google Scholar]
- M. Zlámal, Curved elements in the finite element method II. SIAM J. Numer. Anal. 11 (1974) 347–362. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


